Real-Life Math Applications: from ancient times to today

The oldest known evidence of mathematical work—Babylonian mathematics, which dates back more than 5,000 years—shows that it had both theoretical [10] and practical, application-oriented dimensions [11].

The same is true for ancient Chinese and Indian mathematics. Alongside theoretical developments, it included many practical exercises that emphasized the connection between math and the real world. These exercises covered areas like military strategy, agriculture, construction, and other practical applications.

In the following sections, we’ll explore examples from ancient sources that demonstrate how mathematics was applied in real-world situations during ancient times.

General math

Calculation of unit costs

An example of an ancient Chinese math task is as follows:

“13,500 cash* was spent to buy 2,350 bamboos. What is the price of 1 bamboo?” (Answer: $ 5 \frac{35}{47} $ cash).

* Cash was a currency used in ancient China.

Source: “The Nine Chapters on the Mathematical Art”, Book II, task 33. [15]

This basic exercise resembles arithmetic problems we encounter today. While this task may seem simple to us now, thousands of years ago, it was a significant challenge. Understanding and applying arithmetic to calculate unit costs was particularly difficult in an era without calculators. However, the ability to calculate unit costs was important not only for traders but also for buyers, who needed to perform such calculations to avoid being cheated.

Calculation of manufacturing output

An example of an ancient Chinese math task is:

“1 worker produces 38 roof tiles of one type in 3 days and 76 roof tiles of another type in 2 days. If the worker now produces equal amounts of both types of roof tiles for 1 day, how many roof tiles will the worker produce?” (Answer: 25 and a small half of a tile).

Source: “The Nine Chapters on the Mathematical Art”, Book VI, task 22. [15]

This type of task arises from practical needs—in this case, the need for roof tile manufacturers to predict their output. Such tasks are still relevant today, as production planners at modern factories must determine how many units are produced by machines (or workers) and then predict future production amounts.

Estimation of needed workforce

In ancient construction projects, determining how many workers were required to complete a job was crucial. These calculations not only involved understanding the volume of material (stones, or soil) to be moved but also took into account seasonal variations. Depending on the season, a worker’s output could vary due to weather conditions, affecting how much soil could be processed. The following tasks are examples of practical problems in ancient times where mathematics was used to estimate both the volume of material and the required workforce for construction.

Lower width of a water dam is 2 zhàng, upper width is 8 chǐ*. Height of the dam is 4 chǐ and length is 12 zhàng and 7 chǐ. During the winter construction works, one worker can process 444 chǐ of soil. What is the volume of the dam, and how many workers are needed to build the dam? (Answer: the volume of the dam is 7112 chǐ, and 16 $ \frac{2}{111} $ workers are needed). [15]

* At the time these ancient texts were written, 1 chǐ equaled approximately 9 inches (~0.23 meters). 1 zhàng = 10 chǐ.

Source: “The Nine Chapters on the Mathematical Art”, Book V, task 4. [15]

In this task, the water dam has a trapezoid-shaped cross-section, as shown in the picture below:

What’s interesting about this problem is that it considers both: a) the volume of soil that needs to be excavated and b) the number of workers required to complete the project. Another notable aspect is the term “winter construction,” which means that the season affects worker output. Now, let’s examine a similar problem:

The upper width of a water canal is 1 zhàng and 5 chǐ, and the lower width is 1 zhàng, the depth is 5 chǐ, and the length is 7 zhàng. During spring construction, each worker can dig out 612 $ \frac{4}{5} $ chǐ of soil. What is the volume of the canal, and how many workers are needed to dig it? (Answer: the volume is 4375 chǐ, and 7 $ \frac{427}{3064} $ workers are needed).

Source: “The Nine Chapters on the Mathematical Art”, Book V, task 5. [15].

These problems emphasize several practical elements that are essential for solving them:

First, the volume of soil to be moved must be calculated.
Second, the number of workers required to move the soil must be determined.
Finally, the season of the construction is taken into account, affecting the workforce calculation.

Other similar problems in The Nine Chapters on the Mathematical Art [15] also provide excavation norms for summer and autumn construction (871 and 300 chǐ respectively), further highlighting how these mathematical problems were rooted in real-world construction needs and focused on practical applications.

Area, Perimeter, Circumference

It is widely recognized that geometry originated as a highly practical discipline aimed at solving real-world problems. The word “geometry” itself comes from the Ancient Greek term γεωμετρία (geōmetría), meaning “land measurement,” which reflects its practical roots. Geometry saw remarkable development in regions where the need for its application was especially high. For instance, the historian Herodotus noted that Egyptian geometry emerged from the necessity to fairly redistribute land after the Nile flooded, providing a clear example of geometry’s material origins [16].

Given its strong connection to real-world needs, geometry tasks involving the calculation of area, perimeter, or circumference are some of the most common types of ancient mathematical applications. Below are examples of ancient tasks that involved measuring fields of various shapes.

Calculating the area of a rectangular field

There is a field 12 bù* wide and 14 bù long. What is the area of the field? (Answer: 168 bù²).

* 1 bù (step) in Ancient China was approximately 4.36 ft (~1.33 m). 1 bù = 6 chǐ.

Source: “The Nine Chapters on the Mathematical Art”, Book I, task 2. [15]

Calculating the area of a triangular field

There is a field that is 12 bù wide, with a straight length* of 21 bù. What is the area of the field? (Answer: 126 bù²).

* The height of a triangle in ancient China.

Source: “The Nine Chapters on the Mathematical Art”, Book I, task 25. [15]

Calculating the area of a circular field

There is a circular field with a circumference of 30 bù and a diameter of 10 bù. What is the area of the field? (Answer: 75 bù²).

Source: “The Nine Chapters on the Mathematical Art”, Book I, task 31. [15]

It’s interesting to note that in this calculation, $\pi = 3$. Although the more precise value of $\pi = \frac{22}{7}$ was known to ancient Chinese mathematicians, throughout The Nine Chapters on the Mathematical Art, the value $\pi = 3$ is often used. This shows that this approximation was considered sufficient for practical purposes, as avoiding fractions likely made calculations quicker and easier.

Calculating the size of a field when the area is known

Another common mathematical application in ancient times involved calculating the unknown side of a field when its area was already known. This type of task was likely related to practical situations, such as marking new fields. For example:

There is a field that is 1 and a half bù wide. It is known that the area of the field is 1 mǔ. What is the length of the field? (Answer: 160 bù).

Source: “The Nine Chapters on the Mathematical Art”, Book IV, task 1. [15]

Such exercises were important when new fields needed to be established, for instance, after floods—like the case Herodotus described when fields were redistributed. Calculating the appropriate dimensions based on a given area was essential.

One remarkable aspect of this task is the extreme ratio between the width and length of the field: the width is more than 100 times smaller than its length, meaning the field would appear elongated, resembling the shape of rice fields in ancient China. This may reflect the actual structure of agricultural fields at the time.

Another interesting observation from The Nine Chapters on the Mathematical Art is the absence of tasks involving parallelograms when calculating areas. While the text includes examples of rectangular, square, circular, and even trapezoidal fields, there are no mentions of parallelogram-shaped fields. This likely reflects the fact that parallelogram-shaped fields were uncommon in ancient China, leading to a limited practical need for calculating their area. Once again, this illustrates how real-world needs influenced the development of mathematical problems.

Volume

Calculating volume is a common theme in ancient mathematical texts. One reason for this prevalence is the need to determine volumes for various practical tasks, such as measuring grain piles, horse carts, and the amount of soil needed for construction. Below are some typical examples.

Volume of grain

There is a pile of rice in the corner. The lower circumference of the pile is 8 chǐ, and the height is 5 chǐ. What is the volume of the pile, and how much rice does it contain (i.e., weight)? (Answer: the volume is $35 \frac{5}{9}$ chǐ³, and there is $21 \frac{691}{729}$ hú* of rice in the pile.)

* 1 hú equals 10 dou. The exact amount of 1 dou at the time these texts were written is not known; today, 1 dou is approximately 2.73 gallons (10.35 liters). Interestingly, in this task, the unit of volume hú is used to measure the weight of grain.

Source: “The Nine Chapters on the Mathematical Art”, Book V, task 25. [15]

What stands out in this and similar tasks is the precision regarding the type of grain pile being measured. In this case, the pile is described as being in the corner. This suggests that ancient mathematicians had empirical methods—based on practical experience—for calculating the volumes of different types of grain piles, such as a usual pile, a pile in a corner, or a pile against a wall.

The Nine Chapters on the Mathematical Art provides calculation guidelines for each scenario:

The rule is: take the lower circumference, multiply it by itself, then multiply by height, divide by 36, and take the result once. When the pile is against the wall, divide by 18 and take once. When the pile is in the corner, divide by 9 and take it once. [15]

Similar triangles

Determining distance to an object

One of the key challenges throughout history has been measuring distances, especially when using tools like rulers or measuring tapes wasn’t practical—such as in mountains or at sea. This led to the application of various mathematical techniques. For example, the principle of similar triangles was used to measure the distance to a boat from the shore.

Here’s how the method worked:

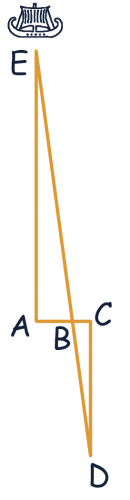
A stick was placed at point $ A $ on the shore, ensuring that the line between the stick and the boat (point $ E $) formed a $ 90^\circ $ angle with the shore.
A second stick was placed at point $ B $, a known distance from point $ A $ (say, 50 feet).
A third stick was placed at point $ C $, some distance away from $ B $ (say, 30 feet), keeping points $ A $, $ B $, and $ C $ in a straight line.
Another stick was placed at point $ D $, making sure that segment $ CD $ was perpendicular to $ AC $ and that the stick at $ B $ lined up with the boat (point $ E $).

As shown in the figure (not included here), two similar triangles are formed: $ \triangle ABE $ and $ \triangle BCD $. To calculate the distance to the boat (segment $ AE $), the following proportion is set up:

\[\frac{AE}{AB} = \frac{CD}{BC}\]

Substituting the known values:

\[\frac{AE}{50} = \frac{300}{30} \Rightarrow AE = 500 \, \text{ft}\]

This method, known as “Thales of Miletus‘ ship problem,” provided a practical way to measure distances when direct measurement was impossible.

But why would ancient people need to measure how far a boat was from the shore? One practical reason could be military: determining the distance to an approaching enemy ship could help in positioning artillery for defense.

Pythagorean Theorem

It is widely believed that the mathematical concept we now call the Pythagorean Theorem was known to the people of Mesopotamia (over 1,000 years before Pythagoras is thought to have lived!). Clay tablets such as YBC 7289 and Plimpton 322 provide evidence of their understanding of the relationships between the sides and the diagonal of a square, as well as Pythagorean Triples. For instance, the diagonal of a square with a side of length 1 was calculated as $ \sqrt{2} $. This knowledge had very practical applications, especially in construction.

Figure: Fresco on the wall of the Ankara museum of Anatolian civilizations showing a man writing on a clay tablet. [13]

Figure: YBC 7289 clay tablet showing ancient Babylonian mathematical calculations, including a geometric diagram and the approximation of the square root of 2.

Construction

Recent studies [11], [12] show that Babylonians applied their understanding of the relationship between the sides of a square and its diagonal when constructing ziggurats—massive buildings resembling temples. One such example is the Tchogha Zanbil Ziggurat (present-day Shushtar, Iran), which has sides measuring 345 feet and a diagonal calculated as $ 345 \times \sqrt{2} $.

Figure: panoramic view of the ziggurat of Tchogha Zanbil. Image: Pentocelo, published under CC BY-SA 3.0.

Manufacturing of Construction Materials

In ancient construction practices, the Pythagorean Theorem also found use in the manufacturing of materials. For instance, consider the following problem:

There is a log with a diameter of 2 chǐ and 5 cùn*. If a rectangular beam with a thickness of 7 cùn needs to be cut from the log, what would be the width of the beam?(Answer: 2 chǐ and 4 cùn.)

* 1 cùn = 1/10 chǐ).

Source: “The Nine Chapters on the Mathematical Art”, Book IX, task 4. [15]

This problem highlights the practical use of the Pythagorean Theorem in optimizing the dimensions of construction materials, ensuring precise measurements for efficient resource utilization.

Military intelligence, landmarking

The Pythagorean Theorem was also applied in military contexts for landmarking and strategic planning. Consider this problem:

There is a square-shaped pond with a side of 1 zhàng. A cattail in the middle reaches 1 chǐ above the water surface. When pulled toward the shore, the cattail touches the edge. What is the depth of the water, and what is the length of the cattail? (Answer: The depth of the water is 1 zhàng 2 chǐ, and the length of the cattail is 1 zhàng 3 chǐ.)

Source: “The Nine Chapters on the Mathematical Art”, Book IX, task 6. [15]

Such problems demonstrate how mathematical techniques, like the Pythagorean Theorem, could have been applied for military intelligence purposes, enabling soldiers or spies to estimate dimensions and distances of landscapes or enemy towns without raising suspicions. These exercises reflect the practical need for accurate spatial measurements in strategic planning.

Fractions

Fractions have played an important role in human activity since ancient times, in fields like trade, agriculture, or construction. The ability to work with fractions allowed people to divide land, measure resources, and perform calculations that required precision beyond whole numbers. For instance, when determining the area of fields with dimensions that were not whole numbers, as can be seen in the following example:

Measuring areas of fields

There is a field that is $ \frac{7}{9} $ bù wide and $ \frac{9}{11} $ long. What is the area of the field? (Answer: $ \frac{7}{11} $ bù).

Source: “The Nine Chapters on the Mathematical Art”, Book I, task 20. [15]

Determining purity of metals

Metals such as copper, silver, and gold, along with their alloys, were widely utilized in Mesopotamia. To determine the purity of these metals, fractions were frequently employed. Below is an excerpt taken from a loan document dated approximately 494 BC [14]:

Širku, son of Iddinaya, owes 1 mina* of silver, with $ \frac{1}{8} $ shekel of alloy to x-iddina, son of Nergal-ušallim […]

* 1 mina is a unit of weight used in Ancient Babylon, equivalent to approximately 1.1 pounds or 500 grams. 1 mina = 60 shekels.

Source: Journal of Ancient Near Eastern History [14]

In this example, the $ \frac{1}{8} $ shekel of alloy specifies that a particular weight of silver includes a fraction (in this case, $ \frac{1}{8} $) made up of alloy. This indicates that the 1 mina of silver borrowed by Širku, son of Iddinaya, contained another metal—likely copper, tin, or other materials that were available and suitable for enhancing silver’s durability or appearance. Using fractions to describe the purity of metals was a common practice in ancient financial operations and agreements, providing a clear understanding of the metal’s composition.

Cooking

There are 5 dǒu and 5 shēng* of proso millet. How much porridge can one get from it?
Rule: When calculating the amount of porridge from proso millet, divide by $ \frac{5}{9} $.
(Answer: There will be 9 dǒu and 9 shēng of porridge).

* 1 shēng = $ \frac{1}{10} $ dǒu

Source: “The Nine Chapters on the Mathematical Art”, Book II, task 17. [15]

In this example, the usage of fractions—specifically, division by a fraction—serves as a means to convert the amount of millet into the volume of food produced. Utilizing fractions in cooking is a common mathematical application, even today. Notably, the resulting volume of porridge, 9 dǒu and 9 shēng (approximately 27 gallons or 102 liters), represents a considerable quantity of food. This may indicate the need to organize catering for a large group of people, such as at a construction site or during a significant event.

Simple and compound interest

Interest has long been an essential concept applied in financial operations, particularly in the practices of lending and borrowing money. This age-old tradition has facilitated trade and economic development across civilizations for thousands of years. The calculation of interest allows lenders to earn a return on their capital while enabling borrowers to access funds needed for various purposes. Below are ancient Mesopotamian mathematical exercises that illustrate the principles of calculating simple and compound interest, reflecting mathematical practices that have endured throughout history:

In what time will the capital that is lent double if the interest rate is 5% per month?

Source: Physical and Mathematical Sciences in Eastern Countries [17]

2) Širku, son of Iddinaya, owes 1 mina of cut-up silver, with $ \frac{1}{8} $ shekel of alloy to x-iddina, son of Nergal-ušallim. At the end of the month Simānu in Babylon, Širku will repay him 1 mina of silver with $ \frac{1}{8} $ shekel of alloy. Starting three months after the month Duʾūzu, interest of one shekel per mina will accrue. Mušēzib-Bēl, son of Aplâ, witnessed the agreement.

Source: Journal of Ancient Near Eastern History [14]

3) Dan-Assur borrows $ \frac{1}{2} $ mina from Pusanum. When Dan-Assur travels to Asur 150 days later, he shall pay back 1 mina of silver. Under this agreement, the borrower shall pay 1 mina in return for $ \frac{1}{2} $ mina of loan he receives; the contract also stipulates that if the repayment fails after 150 days, a new interest rate will be identified, applicable to the prescribed amount of 1 mina. Given that the revenue from the debt transaction over 150 days is 100%, the annual interest rate for this transaction becomes 240%.

Source: A History of Interest and Debt [18]

Conversion of units

In ancient world, the conversion of various units played an important role in daily life and commerce. Understanding how to convert money, weight, area, and even quantities of food was essential for trade, agriculture, and resource management. The following text will explore different types of unit conversions and their practical applications in the ancient world:

Weight

1) You have got 2 talents* and 14 minas of copper. Convert this amount into minas. (Answer: $2 \times 60 + 14 = 134$ minas.)

* 1 talent = 60 minas.

2) 30 minas of copper cost 1/2 mina and 5 šekels of silver. Convert ½ mina and 5 šekels into minas. (Answer: $\frac{1}{2} + \frac{5}{60} \approx 0.5833$ minas.)

Source: A History of Interest and Debt [18]

Area

There is a field that is 15 bù wide and 16 bù long. What is the area of the field in mǔ? (Answer: 1 mǔ)

Source: “The Nine Chapters on the Mathematical Art”, Book II, task 17. [15]

The answer to this task is given in units called mǔ, which was the standard unit for measuring area in ancient China (1 mǔ = 240 sq. bù). Interestingly, the unit of area was defined not as a square but rather as a rectangle of 15 by 16 bù.

Amount of food

Another ancient application of math found in various texts includes numerous mathematical instructions for converting food amounts. These factors were specified for different types of grains, refined and non-refined rice, beans, hops, raw and cooked food, and grains of varying granularity and purity.

For example, it was important to know how much flavor could be extracted from grains based on who would consume it. If one wanted to achieve “very well purified flavor,” the factor used was $ \frac{50}{24} $ (i.e., the amount of grain had to be divided by $ \frac{50}{24} $ to calculate the flavor yield). Conversely, for “flavor for aristocracy,” more purification was required, with the factor changing to $ \frac{50}{21} $:

There is a 7 dǒu and 9 shēng of proso millet. How much flavor for aristocracy can be extracted from it? (Answer: 3 dǒu and $ \frac{39}{50} $ shēng).
The rule: if you want to obtain flavor for aristocracy, divide the amount of proso millet by $ \frac{50}{21} $.

Source: “The Nine Chapters on the Mathematical Art”, Book II, task 3. [15]

There is a dug pit with a volume of 10,000 chǐ. The question is, how much compacted and loose earth will there be separately? (Answer: The compacted earth will be 7,500 chǐ, and the loose earth will be 12,500 chǐ).
The rule: The volumes of the dug pit, loose earth, compacted earth, and removed earth are in the ratio of 4:5:3:4.”

Source: “The Nine Chapters on the Mathematical Art”, Book V, task 1. [15]

These calculations were likely necessary for organizing resources, such as determining how many horse carts would be needed to transport the excavated soil. In “The Nine Chapters on the Mathematical Art”, such ratios of soil amounts are mentioned in relation to constructing town walls, dams, canals, moats, and ditches, highlighting the practical purpose behind these mathematical applications.

Calculating material loss

Image: Women placing silkworms on trays with mulberry leaves during the silk-making process. (Source: Cleveland Museum of Art)

There is 1 jīn* of raw silk, and the loss is 7 liǎngs. There are 23 jīn and 5 liǎngs of raw silk. The question is, what is the total loss? (Answer: 163 liǎngs, 4 zhū and a half.)
The rule: Convert 1 jīn into 16 liǎngs (the divisor). Multiply the 7 liǎngs by the total amount of raw silk in liǎngs (the dividend). Use this to calculate the loss.

Source: “The Nine Chapters on the Mathematical Art”, Book III, task 16. [15]

Weight units involved in this task are as follows:

1 jīn = 16 liǎngs;
1 liǎng = 24 zhū.

The exact weight of 1 jīn during the time of “The Nine Chapters on the Mathematical Art” is unknown, though today it equals approximately 1.102 lb (500 g).

This example demonstrates the cross multiplication method for solving proportions: $\frac{16}{7} = \frac{373}{x}$ — the same method used today. It’s remarkable how proportional calculations, like this one for silk loss, have stayed the same over centuries and are still used in fields such as agriculture, industry, cooking, and finance.

Calculating salary

Another math application comes from an ancient Indian mathematical text:

Image: Pilgrims and a porter with shoulder pole. (Source: Library of Congress)

If a porter receives 9 out of 24 baskets of fruit for carrying them a distance of 5 krośa*, how many baskets will he get if he carries them only for 2 krośa?

* Krośa is an Indian unit of distance, approximately 9,800 ft (3,000 meters).

Source: Physical and Mathematical Sciences in Eastern Countries [17]

Calculating financial gain

A person lent out 1,000 qián, and after one month, the gain was 30 qián. Then, the same person lent out 750 qián and returned it after 9 days. The question is: what is the gain for this second loan? (Answer: 6 ¾ qián)
The Rule: assuming 30 days in a month, use 1,000 qián as the divisor. Multiply the gain of 30 by the amount lent and then by 9 days to find the dividend. Combine the dividend and the divisor to get the final amount in qián.

Source: “The Nine Chapters on the Mathematical Art”, Book III, task 20. [15]

This task demonstrates the application of a complex proportion, also known as the double rule of three. The proportion can be expressed as: $ \frac{30}{300}/1000 = \frac{x}{9}/750 $, which can be simplified to $ \frac{30}{300} \times 1000 = \frac{x}{750} \times 9 $.

Taxation and Duties

In the northern district, there are 8,758 suan*, in the western district 7,236 suan, and in the southern district 8,356 suan. All three districts need to provide 378 people for corvée. The question is: how many people should each district contribute based on the number of suan they have?

Answer:

The northern district must provide 135 and $ \frac{11637}{12175} $ people.
The western district must provide 112 and $ \frac{4004}{12175} $ people.
The southern district must provide 129 and $ \frac{8709}{12175} $ people.

Source: “The Nine Chapters on the Mathematical Art”, Book III, task 5. [15]

*The “suan” is a poll tax introduced in 210 BC by Emperor Gaozu of the Han Dynasty. Every subject between the ages of 15 and 65 had to pay this tax, with 120 people making up 1 suan. In this mathematical problem, the proportional distribution of people for corvée is based on the number of suan in each district.

Calculating prices of metals

If 30 minas of copper cost $ \frac{1}{2} $ mina and 5 shekels of silver, how much silver do you need to pay for 2 talents and 14 minas of copper (134 minas total)? Present the answer in minas and shekels. (Answer: 2 minas and 36 shekels.)

Source: A History of Interest and Debt [18]

Solution:

30 minas of copper = 0.5833 minas of silver.
134 minas of copper = $ x $ minas of silver.

Solving for $ x $ gives us:

\[x = \frac{134 \times 0.5833}{30} = 2.6 \text{ minas of silver}\]

This is equivalent to 2 minas and 36 shekels.

Equations

Quadratic equations

Quadratic equations have their roots in ancient mathematics, with evidence of their use dating back to civilizations like the Babylonians around 2000 BC. These equations were employed to solve practical problems involving areas, volumes, and geometric relationships, particularly in agriculture, architecture, and military engineering. An example of the latter is as follows:

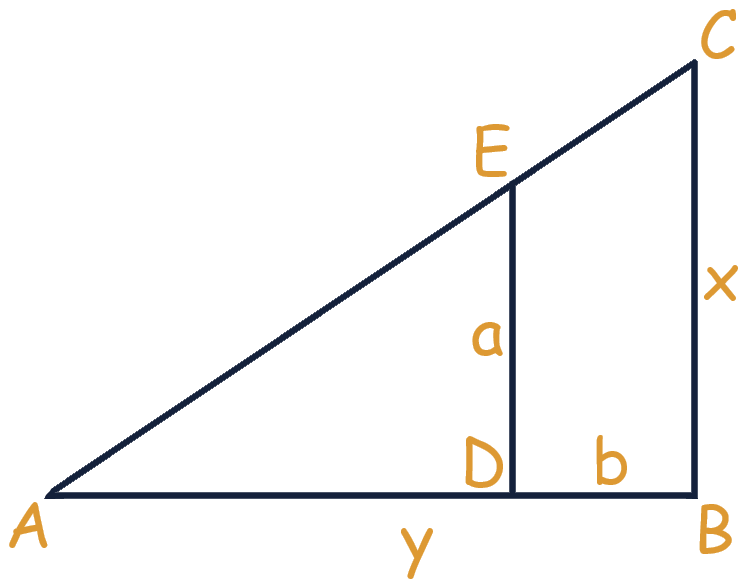
Having 1300 gar of land, I will conquer a city that is hostile to Marduk. I took 6 as the base of the earth mass, 8 as the distance to the wall, and 36 as the height of the earth mass. How long should I flatten to take the city? What is the length behind the slope?”

* In Mesopotamia, the unit “GAR” (also known as “gur” or “kor”) was primarily used for measuring volumes. 1 GAR ≈ 79 gallons (300 liters).

Source: Essays on the History of Mathematics in Antiquity [20]

The task here is to construct a siege ramp (figure above) that the troops could use to climb the wall of the besieged city. The problem mentions the volume of the ramp (1300 gar) and provides the width (6 units of length), height of the built part (a=36), and the remaining distance to the wall (b=8). It is necessary to calculate the height of the wall (x) and the base of the entire ramp (y). The solution to this task involves solving the quadratic equation: $ bx^2 – 2Sx + 2sa = 0 $, where $ S $ is the area of the cross-section of the siege ramp.

Although this problem may seem somewhat artificial in nature (in practice, when constructing a ramp, one must first determine its base, height, and width, rather than the volume of the earth mass), it is nonetheless related to actual military preparations. Ancient military practices anticipated sieges, and the necessary materials, resources, and their logistics were planned in advance [21]. This serves as a striking indicator of the connection between mathematics and practical human activities; in particular, the needs of war led to the emergence of problems of this kind. Among ancient problems involving quadratic equations, there is a whole series related to earthworks.

In addition to the above, look at the two illustrations below. This is the siege of Masada by the Romans, where a siege ramp of exactly this type, as discussed in the mathematical problem, is being constructed. Building such a ramp in ancient times took approximately 2–3 weeks and was carried out by 2,000 to 3,000 soldiers [21].

Image: Roman soldiers climbing the ramp to the ancient fortress of Masada (Source: Customs and Traditions of the Canadian Military Engineers [25])

Image: Aerial view of Masada with the remains of the ancient Roman siege ramp (Photo: Samir Smier)

Military intelligence, landmarking

Evidence suggests that equations of high orders were used in the ancient world. The following mathematical problem comes from ancient China and may have had military applications, such as reconnaissance in enemy territory or landmarking objects.

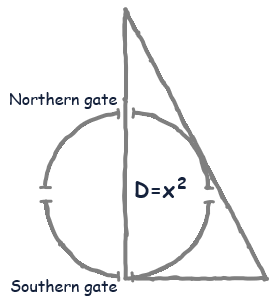
Image: Task illustration

A circular city wall has four gates. Three li away from the northern gate, there is a tall tree. If one exits through the southern gate, turns left, and walks 9 li, the tree becomes visible. How can one determine the circumference and diameter of the wall? (Answer: The diameter is 9 li, and the circumference is 27 li*)

* The value $\pi = 3$ is often used in ancient Chinese mathematical texts. This approximation was likely considered sufficient for practical purposes.

Source: Mathematics of Ancient China [19]

Remarkably, this math problem was solved using a 10th-order equation:

\[x^{10} + 15x^8 + 72x^6 – 864x^4 – 11664x^2 – 34992 = 0\]

This highlights the advanced level of mathematical development in the ancient world.

Systems of equations

Common buying of things (system of linear equations)

People are collectively buying an item. If each person contributes 8, there will be an excess of 3. If each person contributes 7, there will be a shortage of 4. The questions are: how many people are there, and what is the cost of the item? (Answer: There are 7 people, and the cost of the item is 53.)

Source: “The Nine Chapters on the Mathematical Art”, Book VII, task 5. [15]

Although this task is presented in a universal and abstract form, its practical application in ancient societies could relate to taxation or contributions for public projects. This type of calculation might determine how much each household or individual should contribute to community initiatives, such as building a well, fortifications, or a temple. The task could help allocate contributions fairly based on the surplus or shortage left after each person or household contributes a certain amount.

Functions

Mathematical functions first appeared in ancient times as a way to represent relationships between different quantities. Early civilizations needed these functions to solve practical problems, such as calculating areas, volumes, and growth rates. Over time, the development of functions paved the way for more complex problem-solving – such as performing complex calculations:

Faster calculations

In ancient times, complex calculations – like finding square or cubic roots – were time-consuming, and people sought ways to perform these calculations more efficiently and accurately. One example from Ancient Greece illustrates how they addressed the practical need for complex calculations.

One common application of the cube root was finding the side length of a cube when the volume was known. This knowledge was especially useful for tasks like digging a cube-shaped water reservoir with a desired volume. Today, calculating the side length of such a reservoir is straightforward with calculators, but in ancient times, it posed a challenge.

The ancient Greek mathematician Menaechmus discovered a method to precisely calculate the cube root using conic sections. In modern notation, to find the cube root of a value $ a $, one would create a parabola (the graph of a quadratic function) given by $ y = x^2 $ and a hyperbola (the graph of a reciprocal function) defined as $ y = \frac{a}{x} $. The intersection of these two curves yields the cube root of $ a $. For example, to determine the side length of a cube-shaped water reservoir with a volume of 2000 gallons (i.e., $ x = \sqrt[3]{2000} $), one would construct the parabola $ y = x^2 $ and the hyperbola $ y = \frac{2000}{x} $. The intersection of these graphs provides the solution, which in this case is $ x \approx 12.599 $.

Image: Intersection of the parabola $y = x^2$ and hyperbola $y = \frac{2000}{x}$ at approximately x≈12.599 and y≈158.74

Trigonometry

Measuring time

Trigonometry emerged from the need to measure time, particularly the day and the precise time of year. In the ancient world, timekeeping relied heavily on tracking the movement of the Sun. To do this, people used a device called a **gnomon**—an early astronomical instrument designed to measure the Sun’s angle. By dividing the length $ L $ of the gnomon by the length of its shadow $ l $, they could calculate the angular height $ \alpha $ of the Sun above the horizon:

\[\tan(\alpha) = \frac{L}{l}\]

Image: Gnomon and its shadow, showing the $L/l$ relationship.

Animation: the movement of a shadow around a gnomon.

Since the Sun rises at different angles throughout the year, people studied the $ L/l $ relationship—essentially early trigonometric ratios. This helped them define the time of day, length of the year and cardinal directions, track seasons, and identify solstices. These studies eventually evolved into a field called Gnomonics, which laid the foundation for trigonometry.

Ancient math applications - conclusion:

While some mathematical applications from ancient times no longer apply to the modern world—such as calculating the side of a town wall, measuring the depth of water, or determining the distance to a ship—many ancient mathematical practices remain relevant to our daily lives:

We still calculate expected financial gain, much like the ancient Mesopotamians did.
Calculating the area of land is still done in much the same way as it was in antiquity.
Proportions are still commonly used in cooking recipes today.

In professional fields, some mathematical methods have persisted for thousands of years:

The method for determining a 90° angle in construction is still often used, as it was in Mesopotamia and Ancient China.
Catering services still calculate food yield from raw ingredients, similar to ancient practices.
Modern workforce planning often mirrors how labor was calculated in the BC era.

Some mathematical applications, like using functions to calculate roots or employing trigonometry to track the movement of the Sun, may seem outdated. But does that mean this mathematical knowledge has become obsolete?

Before answering, take a look at the images below.

Image: MarsDial on the Spirit rover on Mars.

On the left is a picture of the Spirit/Opportunity Mars Exploration Rover, which landed on Mars in January 2004. In the red circle, you’ll notice a small pole called the MarsDial, which acted as a gnomon to measure the Martian day and track the Sun’s movement throughout the year. The shadow of this gnomon was transmitted back to Earth, allowing NASA specialists to define the time of day and cardinal directions—in the same way as it was done several thousand years ago! On the right, you see the gnomon in action on Mars. This demonstrates that ancient mathematical knowledge and its real-life applications remain relevant, even after thousands of years!

Next, we’ll explore mathematical applications from the AD era, spanning from the 1st to the 19th century.

Math applications from the 1st to the 19th century

↑ Back to Math applications from the 1st to the 19th century

Throughout the AD era, everyday tasks—such as measuring fields, calculating wages, handling taxation, and construction—continued largely unchanged, leading to increasingly widespread use of mathematics for solving these practical issues. This period saw the emergence of numerous books on applied mathematics. Of particular note was the publication of mathematical texts not only in Latin (like Practica Geometriae, 1221) but also in local languages, aimed at merchants, financial officials, surveyors, craftsmen, and builders. For example, A Book on Those Geometric Constructions Necessary for a Craftsman (ca. 980-990) provided guidance on practical arithmetic and geometry. These texts included step-by-step problem-solving rules and numerous specific tasks to guide readers.

With the growing complexity and volume of calculations, two significant developments occurred: 1) the rise of professional “calculators” — people whose job was to carry out calculations, and 2) the advancement of calculation devices, which evolved to handle increasingly large numbers.

Let’s explore some specific mathematical applications that emerged during this period.

Number theory

Mechanical calculators

While studying number theory might not seem obviously useful, it plays an important role in understanding how numbers work. In the Middle Ages, knowing key ideas in number theory, like prime and composite numbers, Greatest Common Factor (GCF), and Least Common Multiple (LCM), helped people develop better ways of calculating. For example, Fibonacci’s work with the base-10 system eventually led to early mechanical calculators. These machines used gears marked with numbers, where each gear would move the next one forward after making ten turns—an early method of automated calculation.

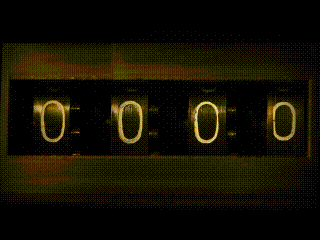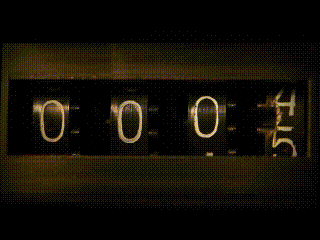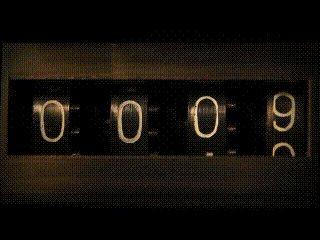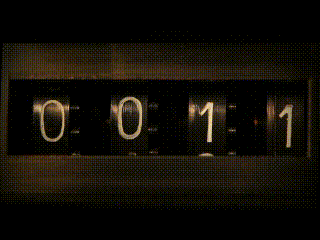
Image: Pascal’s mechanical calculator. (Photo: David.Monniaux, CC BY-SA 3.0)

Angles

Ballistics

Ballistics is the study of the movement of projectiles, like bullets and cannonballs, through the air. This field focuses on how these objects travel and what factors affect their paths. Geometry plays a crucial role in ballistics, especially when it comes to understanding angles.

In the 1530s, Italian mathematician Nicolo Tartaglia conducted research on the paths of projectiles. He looked at how the range of a projectile changed depending on the angle it was fired. Military forces began using this knowledge to position cannons at specific angles for better accuracy.

In the figure above, you can see a representation of a cannon aimed at a 45-degree angle, as shown in Nicolo Tartaglia’s book. This angle is significant because it often provides the best balance between height and distance for a projectile’s range.

↑ Back to Math applications from the 1st to the 19th century

Equations

Division of inheritance (linear equations)

One interesting application of equations occurred in the Islamic world, particularly in the division of inheritance. Islamic law has specific rules for how inheritance is distributed among heirs, including daughters, parents, grandparents, spouses, and siblings. Let’s look at an example.

Suppose a man passes away, leaving behind an estate worth 1,000 gold coins. He has three heirs: a wife, a son, and a daughter. According to Islamic inheritance laws, the wife receives $ \frac{1}{8} $ of the estate, while the son receives twice the portion of the daughter.

Wife’s Share:

\[ \text{Wife’s share} = \frac{1}{8} \times 1000 = 125 \text{ coins} \]

Remaining Estate:

\[ \text{Remaining} = 1000 – 125 = 875 \text{ coins} \]

Son and Daughter’s Shares:

Let the daughter’s share be $ x $. Therefore, the son’s share would be $ 2x $.

The total for the son and daughter will be:

\[ x + 2x = 3x = 875 \]

From this linear equations, we can find $ x $:

\[ x = \frac{875}{3} \approx 291.67 \] (daughter’s share)

The son’s share is:

\[ 2x = 2 \times 291.67 \approx 583.33 \] coins.

↑ Back to Math applications from the 1st to the 19th century

Ruler and Compass Constructions

Architecture

Persian mathematician Abu al-Wafa’ al-Buzjani, in his work A Book on Those Geometric Constructions Which Are Necessary for a Craftsman, outlined specific instructions for craftsmen on creating geometric shapes and patterns. Many of these techniques were widely used in the architecture of the Islamic world.

In the figures below, you can see an example: on the left is the division of a circle using a compass and ruler on paper, and on the right is an architectural ornament created using this technique.

In the figures, you can see an example: on the left is a photocopy from the original work of al-Buzjani (Istanbul manuscript, [17]), featuring drawings of circles and multi-sided polygons created with a ruler and compass. Below is an architectural ornament created using this technique.

↑ Image: photocopy from the original work of al-Buzjani (Source: Physical and Mathematical Sciences in Eastern Countries [17]).

→ Image: Decorated stone in Hisham’s Palace, Palestine (Photo: Michael Darter, CC BY-SA 3.0)

↑ Back to Math applications from the 1st to the 19th century

Negative numbers

Negative numbers were known in ancient China and typically referred to debt or a shortage of something [19]. Indian mathematicians also recognized negative numbers, interpreting them as segments heading in opposite directions [22]. In Islamic countries, negative numbers appeared later and were used in multiplication methods, as described below.

Faster calculations

As the need for multiplication grew, mathematicians worked on faster and better methods to perform it. The Persian mathematician Abu al-Wafa’ al-Buzjani developed a rule for multiplying two numbers, as follows (example is given for (16 * 18)):

Step 1: Subtract the difference between the second number and the next multiple of ten from the first number: $ 16 – (20 – 18) = 16 – 2 = 14 $

Step 2: Multiply the result from Step 1 by the multiple of ten you used: $ 14 \times 20 = 280 $

Step 3: Subtract the first number from the next multiple of ten, and do the same with the second number. Then multiply these two results: $ (20 – 16)(20 – 18) = 4 \times 2 = 8 $

Step 4: Add the result from Step 3 to the number you got in Step 2: $ 280 + 8 = 288 $

So, indeed, $ 16 \times 18 = 288 $.

While using this multiplication method, Abu al-Wafa’ noticed that the rule also worked when the difference from Step 1 was negative. For example, let’s multiply 3 by 5:

Step 1:
$ 3 – (10 – 5) = -2 $
(This is the first known use of negative numbers in the Islamic world!)

Step 2:
$ -2 \times 10 = -20 $

Step 3:
$ (10 – 3)(10 – 5) = 7 \times 5 = 35 $

Step 4:
$ 35 + (-20) = 15 $
Answer: $ 3 \times 5 = 15 $

Why is this use of negative numbers noteworthy? In Ancient China and India, negative numbers were mainly used to represent concrete concepts like debt or shortage. This meant they served a practical purpose. However, in Abu al-Wafa’s work, negative numbers were treated as an abstract mathematical tool. They were used as an intermediate step in calculations, similar to how we use parentheses today. This was a remarkable advancement in mathematics at the time.

↑ Back to Math applications from the 1st to the 19th century

Trigonometry

Astronomy

Trigonometry played an increasingly important role in observing the Sun, Moon, stars, and planets. Beyond scientific purposes, these observations were also practical, as they helped with measuring time and navigation, as well as determining the times of sunrise and sunset. All of these tasks required greater precision in calculating the values of trigonometric functions.

As a result, special tables with values for sine, cosine, tangent, and other trigonometric functions were created and continually refined for accuracy.

For instance, mathematicians in the Islamic world focused on calculating sin(1°) using various methods. In the 15th century, the Persian mathematician Jamshid al-Kashi achieved an extraordinary milestone by calculating the value of sin(1°) with precision up to the 17th decimal place in the contemporary decimal system. This was a remarkable accomplishment for that time and was essential for precise navigation, such as on ships at sea. An example of how these tables were used is described in the next section.

↑ Back to Math applications from the 1st to the 19th century

Navigation

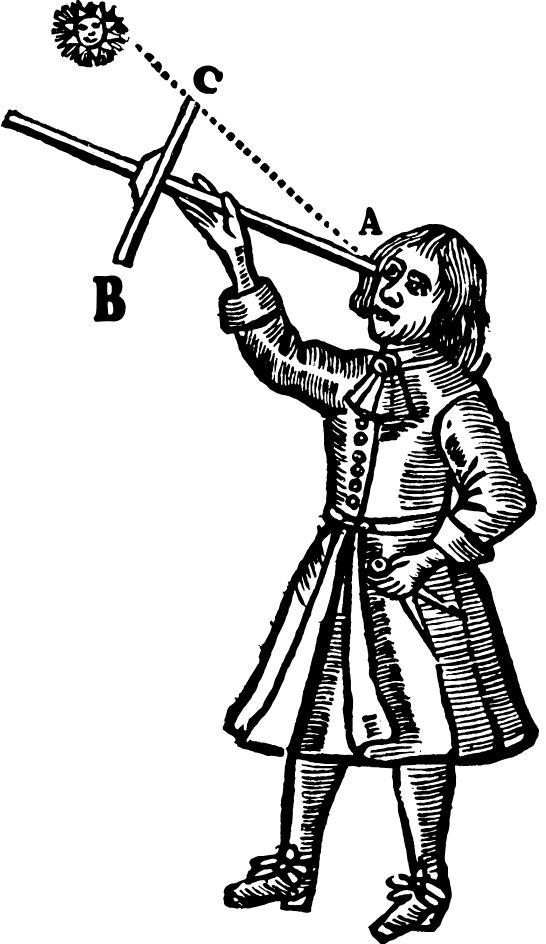
One of the simplest yet effective devices for navigation in the Middle Ages was the Jacob’s staff—a graduated pole with a perpendicular and movable crossbar.

To use it, the navigator would place one end of the main staff against their cheek, just below the eye [A]. By sighting the horizon through the lower part of the transom (or through a hole in the brass fitting) [B], they would then adjust the crossbar on the main staff until the Sun is at the other end of the transom [C]. The altitude of the Sun could then be determined by reading the position of the crossbar on the scale of the main staff. This value was converted to an angular measurement using a table created with the help of trigonometric calculations.

↑ Back to Math applications from the 1st to the 19th century

Ratios and proportions

Lifting machines (#1)

As mechanics developed, people began building machines to assist in construction, such as those for lifting bricks, mortar, and other heavy objects. One of the simplest machines for lifting objects is the lever.

Image: The lever (Source: Theory and Practice in Heron’s Mechanics [26])

It is well known today that if the ratio of the length of the longer arm (BD) to that of the shorter arm (DA) equals the ratio of the weight (G) to the moving force applied at point B, the lever is in equilibrium. If the ratio is greater than $ \frac{G}{B} $, the force will lift the weight:

\[\frac{\text{BD}}{\text{DA}} = \frac{G}{B}\]

Hero (Heron) of Alexandria made significant contributions to the calculations necessary to understand how this system works, enabling the construction of more complex machines capable of lifting substantial weights. An example of this is described in the following paragraph.

Lifting machines (#2)

Understanding how levers can help lift heavy objects led people to create more complex mechanisms and machines for lifting. One such machine consisted of two concentric wheels, as shown in the figure below. Knowledge of diameters and circumferences was essential for designing machines capable of lifting the required weights. In one of Heron’s works, he described the Baroulkos machine, which uses toothed wheels to lift a weight of 1,000 talents (about 57,320 pounds/26,000 kilograms) while applying a force of only 5 talents (ca. 287 pounds/130 kg) – a 1:200 ratio!.

Image: Lifting machine capable of lifting about 57,320 pounds (Source: Theory and Practice in Heron’s Mechanics [26])

↑ Back to Math applications from the 1st to the 19th century

Statistics

Cryptography

François Viète, a French mathematician, famously broke a cryptographic code used by the Spanish during the reign of Henry IV of France in the late 16th century. The Spanish used a cipher system to send secret messages during their conflict with France. It’s believed that he employed frequency analysis—a mathematical technique in cryptography that compares the frequency of letters in the cipher with the typical frequency of letters in the language being used (in this case, Spanish). For instance, in most languages, certain letters, like “E,” are more common. By statistically analyzing the patterns of occurrence, Viète could make educated guesses about which letters corresponded to which in the cipher.

Here’s a simplified example of how this works:

Let’s say we have an encrypted message in Spanish where the phrase “el militar” (meaning “soldier” in Spanish) is hidden using a simple substitution cipher. Here’s a step-by-step breakdown:

Identify the common letters: In Spanish, the most frequent letters are e, a, and o. If our encrypted message has a lot of a particular symbol, that symbol is likely to correspond to one of these letters.
Look for common words: In Spanish, “el” (the) is the most frequent two-letter word. If we see any two-letter patterns repeating in the encrypted text, they could be potential candidates for “el.” Likewise, “militar” has repeated letters like i, which could help pinpoint frequent symbols.

3. Apply known patterns: Let’s say the encrypted word for “el militar” is represented as “ZN BQNQMOE.”

- We would look at the frequency of each letter. If “ZQ” appears often, we can assume it could be “el.” Moreover, if “Z” appears frequently throughout the text, it is an additional indicator that it could be “E,” since “E” is among the most frequent letters in Spanish.
- The sequence “BQNQMOE,” a seven-letter word, could represent “militar,” because the message is obviously of military topic. It’s of similar length, its 3rd letter is L (because we already know “ZN” is “el,” so L corresponds to N), and 2nd and 4th letters are the same (I corresponds to Q).
- If “B” represents m, we continue analyzing letter patterns based on typical Spanish letter frequencies.
Trial and error: Substituting likely letter frequencies and trying different combinations, we can piece together the message until it matches a known phrase.

By identifying high-frequency letters and recognizing word patterns, especially those common in Spanish, we can use statistical analysis to break down the encryption. This process is rooted in the algebraic understanding of frequency distributions and substitution patterns.

↑ Back to Math applications from the 1st to the 19th century

Conclusion:

As shown in the section on mathematical applications from the 1st to 19th century, many societal needs stayed the same: marking land, construction, cooking, astronomy, navigation, manufacturing, and finance. Because of this, many mathematical applications also remained similar.

However, it’s important to note that these applications began to shift towards helping people avoid hard physical work. Mathematics started to play a role in building machines, like lifting devices. Another noticeable change was how math helped reduce routine tasks, such as calculations, leading to the creation of the first mechanical calculators.

So, while many needs stayed the same, mathematical applications evolved to make life easier. This shift eventually resulted in more advanced methods and devices. In the late Middle Ages, science became more practical, focusing on technology and everyday life. This period saw the rise of the first firearms, crank mechanisms, better engines powered by animals, water, and wind, distillation techniques, and the invention of mechanical clocks. Finally, the Age of Discovery opened up new horizons in math applications.

Building on the rich history of mathematical applications from the 1st to the 19th century, we can now explore how mathematics continues to shape our daily lives in modern times.

↑ Back to Math applications from the 1st to the 19th century

Today’s math applications

↑ Back to Main Sections

This section covers modern math applications from the 20th century to the present. Browse the list of topics and click on the mathematical subject that interests you (e.g., trigonometry, probability, etc.). Each section provides a general overview of the application, and if you’d like to learn more, you can visit our full article for a detailed description or watch the short video preview.

Algebraic and rational expressions

Faster calculations

Simply put, algebraic and rational expressions are used in computer technology to make computers run faster. For example, if a computer is asked to calculate the expressions: \[\frac{(a+b)^2}{a+b}\] and its simplified form $(a+b)$, then the simplified one takes less computing time and electrical energy. To create efficient computer programs, this kind of simplifying is crucial—especially for computer programs working in critical systems like car safety, air traffic control, and battery-powered devices.

On the left (or above, if you are on the mobile screen) there is a preview of related educational video for K-12 students. There is also a longer text version of this math application available in our article ‘Algebraic and Rational Expressions: A Real-Life Example from Computer Technology‘.

Area, Perimeter, Circumference

Microbiological studies

Calculating circumference is crucial in microbiology for measuring bacterial growth. Researchers use the formula $c = 2 \pi r$ to analyze bacteria like E. coli. By measuring the perimeter of a bacterium’s cross-section, they can track its growth, which is important for developing effective antibiotics.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Circumference: A Real-Life Example from Microbiology.

Water supply

Calculating the area of composite figures is important in water supply management. For example, specialists measure the cross-sectional area of water canals to determine flow rates. Using the formula for a composite shape, which combines rectangles and triangles, they can calculate the area and apply it to manage water resources effectively. This process is vital for ensuring sustainable water supply and management.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Area of Composite Figures: A Real-Life Example from Water Supply.

Cartesian coordinate plane

Medical analysis

The Cartesian coordinate plane is a valuable tool in medicine for organizing data, such as how lifestyle choices impact health. For example, doctors analyze lung cancer survival rates using a graph that shows survival percentages over time for smokers versus non-smokers. This visual helps in understanding the effects of smoking on health and guides better medical decisions.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Coordinate Plane: A Real-Life Example from Medicine.

Equations and inequalities

Cybersecurity in social media

Mathematical inequalities are crucial in cybersecurity, especially for identifying malicious social bots on social media. By analyzing the ratio of followers to friends on accounts, experts can flag suspicious profiles. For instance, if an account has a followers-to-friends ratio that is greater than (or less than) the usual benchmark, it may be deemed suspicious. This approach helps in protecting users from bots that spread misinformation.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, How to Write Inequalities: A Real-Life Example from Social Media.

Wildfire protection

Understanding equations and dependent and independent variables is essential in fire protection, especially for predicting fire spread. For example, fire spread speed depends on factors like the type of fuel and wind strength, which are independent variables. Fire specialists use special equations to calculate how fast a fire will spread. This knowledge helps improve response strategies during wildfires.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Dependent and Independent Variables: A Real-Life Example from Fire Protection.

Geometry of angles

Architecture

Understanding angles is crucial in architecture, especially for designing energy-efficient buildings of the XXI century. For example, architects determine the optimal angle for solar panel reflectors to maximize sunlight exposure. By applying the principles of adjacent and alternate angles, they can ensure that sunlight is effectively directed to the solar panels. This knowledge not only enhances energy efficiency but also integrates renewable energy solutions into building designs.

Civil engineering

Calculating central angles is essential in civil engineering, particularly for designing curved roadways. When civil engineers plan a road curve, they determine the degree of curvature, which helps ensure safe driving conditions. Understanding these angles allows engineers to comply with regulations and implement safety measures, such as adjusting speed limits or installing guardrails.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, How to Find a Central Angle: A Real-Life Example from Civil Engineering.

General math

Collaborative robotics

Math and psychology come together in smart technology to interpret human emotions. For example, systems like drowsy driver detection analyze facial expressions and eye movements to monitor alertness. Using special cameras, these systems convert facial cues into mathematical codes, enabling computers to recognize states of drowsiness or fatigue. This integration of psychology and math enhances safety in vehicles and other smart applications.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Psychology and Math: A Real-Life Example from Smart Robots.

Inverse trig functions

Forensics

Arctan, or inverse tangent, is crucial in criminology for reconstructing crime scenes, especially to determine shooting angles. Forensic scientists use arctan calculations to analyze bullet trajectories. This mathematical approach helps them piece together the events of a crime, leading to more accurate investigations.

Functions

Public health system (piecewise linear function)

Piecewise linear functions are important in public health for analyzing stress levels, especially after traumatic events. By modeling data for different age groups, specialists can predict how many people might need psychological support in the future. This forecasting helps ensure that resources, like psychologists, are available when needed, enhancing community health responses.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Piecewise Linear Functions: A Real-Life Example from Public Health.

Entertainment industry (linear function)

Linear functions are used in entertainment industry, particularly for managing lighting during performances. Lighting specialists use these functions to control luminosity of stages, ensuring smooth transitions in brightness. For instance, they can adjust how quickly a light fades in or out, enhancing the overall experience for the audience.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Linear Functions: A Real-Life Example from Entertainment.

Public health system (quadratic function)

Parabola equations help public health experts predict mental health needs after traumatic events, such as PTSD trends over time. By analyzing stress levels in different age groups, specialists can forecast the potential need for psychological support, ensuring resources are available in affected areas.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Parabola Equation: A Real-Life Example from Public Health.

Lines, line segments, and rays

Archaeology and forensics

Parallel and perpendicular lines are essential in forensics and archaeology, especially for reconstructing facial features from skulls. By aligning lines at specific angles, experts can estimate the shape of features like the nose, providing insight into the likely appearance of individuals from the past.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Parallel and Perpendicular Lines: A Real-Life Example from Forensics and Archaeology.

Negative numbers

Agriculture

Negative numbers are valuable in agriculture, especially for monitoring pests. Digital sensors detect small vibrations pests create when feeding. By analyzing changes in vibration intensity—often measured with negative numbers—farmers can assess pest movement and the effectiveness of pesticides. This method provides insights into pest behavior and helps reduce crop damage.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Negative Numbers: A Real-Life Example from Agriculture.

Weather forecast

Negative numbers are vital in weather forecasting, especially for predicting thunderstorms. Meteorologists calculate special atmospheric indexes, which involve subtracting negative numbers to measure atmospheric instability. A more negative index indicates a higher chance of storms, aiding meteorologists in creating accurate weather alerts.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Subtracting Negative Numbers: A Real-Life Example from Weather Forecasting.

Percent and percentage

Business development

Businesses often use percentages to analyze data and make informed decisions. For example, a company might examine installation rates of its app on different devices, comparing user engagement across platforms like Android and iOS. By understanding these rates, the business can allocate its development budget effectively to meet user demand.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Percent Problems: A Real-Life Example from Business.

Legal

Percent calculations help assess the reliability of self-driving cars in legal cases. Lawyers compare the error rates of autonomous vehicles to those of human drivers, using percentages to determine liability in accidents. This analysis supports fair rulings when new technologies are involved.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Percent Problems: A Real-Life Example from Legal Cases.

Polynomials

Marketing

Polynomials are used in marketing for understanding customer behavior. By analyzing feedback on different aspects of a product or service, companies can gain insights into overall customer satisfaction. Adjusting how they weigh these factors allows marketers to see how changes might influence customer perceptions and improve their strategies.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Polynomials: A Real-Life Example from Marketing.

Data analysis

Polynomial graphs are important in data analysis for understanding trends. For instance, website owners use them to track and analyze their visibility in search engines like Google, making it easier to spot patterns and optimize their online presence. Using polynomial trendlines in tools like Excel, data analysts can determine whether a webpage’s ranking is rising, falling, or fluctuating, providing valuable insights for strategic decision-making.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Polynomials: A Real-Life Example from Data Analysis.

Probability

Artificial Intelligence

In Artificial Intelligence, probability is crucial for tasks like machine translation. For example, when translating sentences, algorithms determine the most likely meaning of words based on their usage in context. By analyzing word pairs, like “dog” and “bark,” these systems can choose the correct translation more accurately. This method helps AI software improve its translations.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Theoretical Probability: A Real-Life Example from Artificial Intelligence.

Digital design (UX design)

Theoretical probability is crucial in digital product design, especially in music streaming services that recommend songs. These platforms analyze user listening habits to provide personalized suggestions. For example, a service may start with a large song database and narrow down recommendations based on user preferences, significantly increasing the chances of offering songs the user will enjoy. This process helps enhance user experience and improves overall recommendation accuracy.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Theoretical Probability: A Real-Life Example from Digital Design.

Pythagorean theorem

DIY

The converse of the Pythagorean theorem is valuable in DIY projects, particularly in construction and carpentry. It helps ensure that angles are precisely 90 degrees when building structures. For example, when constructing a foundation, workers can check if the longest side of a triangle formed by the dimensions matches the required length. This technique is widely used to create right angles in various building projects.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Pythagorean Theorem Converse: A Real-Life Example from DIY.

Mechatronics

The Pythagorean theorem is essential in mechatronics, particularly in creating advanced medical devices like exoskeletons. This theorem helps engineers ensure precise movements in these systems. The Pythagorean theorem is a key principle that guides this accuracy, showcasing how basic math concepts are applied in high-tech environments.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, 3-4-5 Triangle: A Real-Life Example from Mechatronics.

Radicals

Nanotechnology (cube root)

Cube roots are essential in nanotechnology for measuring nanoparticle sizes, often less than 100 nanometers. Engineers calculate the side length of cube-shaped nanoparticles using their volume, derived from mass and density. This approach demonstrates the application of math, physics, and chemistry, enabling precise control over nanoparticle properties and leading to advancements in materials science and pharmaceuticals.

Statistics

Marketing

Simpson’s Paradox highlights how statistics can be misleading when combining data from different groups. In marketing, initial analysis may suggest one group performs better, but a closer look can reveal a different story when considering context. This example shows the importance of careful statistical interpretation, reminding us that data can sometimes tell conflicting stories.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Simpson’s Paradox: A Real-Life Example from Marketing.

Systems of equations

Self-driving cars

Understanding systems of linear equations is key in self-driving car safety. For instance, these equations help predict when a self-driving car can safely overtake another vehicle on the road. By analyzing the speed and distance of cars using mathematical models, the self-driving car can determine the best time to make the maneuver, ensuring safety for everyone on the road.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Systems of Linear Equations: A Real-Life Example from Self-Driving Cars.

Units conversion

Healthcare (time units conversion)

Unit conversions are essential in nursing for ensuring accurate dosage calculations. Nurses often need to convert between different units of time or volume to administer medications or fluids correctly. Mastering these conversions is vital for delivering safe and effective patient care.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Converting Units: A Real-Life Example from Nursing.

Trigonometry

Oil & Gas

Trigonometry is vital in the oil and gas sector, particularly when drilling wells. Professionals use trigonometric calculations to determine the true vertical depth of inclined wells, which helps ensure accurate drilling. By applying the cosine function, they can measure the depth of the drill bit even when it’s not directly visible. This mathematical approach enhances efficiency and safety in oil extraction processes.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, CosX: A Real-Life Example from Petroleum Engineering.

Robotics

In robotics, understanding trigonometry is key for precise movements. For example, a drilling robot calculates the position of its drill point using right triangles. By modeling the robot’s moving parts as straight lines and applying trigonometric principles, it determines the lengths of missing sides, ensuring accuracy. This demonstrates how math can effectively address real-world challenges in technology.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Finding the Missing Side: A Real-Life Example from Robotics.

Vectors

Computer games (vector addition)

Vectors are essential in game development, especially for character movement and physics. They help define direction and speed, allowing for realistic animations and interactions. For instance, when a character moves or jumps, vectors calculate their trajectory and position in a 3D space. This mathematical concept is crucial for creating immersive gaming experiences.

To the left (or above on mobile), you’ll find a related educational video preview for K-12 students. You can explore a longer text version of this math application in our article, Vectors: A Real-Life Example from Game Development.

Today's math applications - conclusion:

Like in ancient and medieval times, today’s math applications still support society’s basic needs: food production, construction, manufacturing, transportation, healthcare, and trade, among others. In the past two centuries, math has also expanded into areas like safety, security, and entertainment. While math applications have become more complex, their purpose remains focused on fulfilling human needs that have stayed consistent over time—both physical needs (like food, shelter, and security) and spiritual needs (such as entertainment).

It’s also worth noting that math has long been applied to meet spiritual and cultural needs, covering artistic, religious, and even political aspects. The next section will explore these in greater detail.

Some special math applications

Artistic aspects of math applications

Geometrical projections in art

Throughout history, artists have often drawn inspiration from mathematics. A well-known example is Hans Holbein the Younger’s 1533 painting The Ambassadors, which features an anamorphic image of a human skull created through geometric projection. This skull appears distorted when viewed head-on, but from high on the right side or low on the left, it resolves into a realistic image. The painting may have been intended to hang in a stairwell, where people ascending the stairs would catch a glimpse of the skull from the ideal angle, creating a dramatic effect.

Cultural aspects of math applications

Measuring musical harmony with ratios

Image: Woodcut showing Pythagoras with bells, a kind of glass harmonica, a monochord and (organ?) pipes in Pythagorean tuning. From Theorica musicae by Franchino Gaffurio, 1492 (Source: Bibliothèque nationale de France)

The Pythagorean school held that mathematics and numbers could explain the entire universe, which led them to apply mathematical principles to music. Pythagoreans sought to understand why people find certain melodies enjoyable and what makes music pleasing to the ear.

Using strings as an example, Pythagoras discovered that two strings of the same material and tension will produce harmonious sounds when their lengths form ratios of 1:2, 2:3, or 3:4. Practically, this means that on a guitar, for example, if a full-length string note is played followed by the same string pressed at half, two-thirds, or three-quarters of its length, the resulting sounds will be pleasing.

In musical terms, these ratios relate to notes within the same register. For example, in the “C” register, this would include notes like different octaves of “C” and combinations such as “C,” “G,” and “F.” These notes often appear together in popular melodies, like “Happy Birthday to You,” which uses just three chords: C, G7, and F.

Assessment of intellectual level of officials

In Ancient China, mathematics held great prestige. It was widely believed that a well-educated person should have a solid understanding of mathematics. To secure a government position, officials were required to pass a mathematics exam, alongside assessments in other subjects. They had to demonstrate their problem-solving skills using classical mathematical problems. [19]

Religious aspects of math applications

Throughout history, mathematics has served not only practical needs, like counting and measuring, but also religious purposes, such as rituals aimed at interpreting the will of the gods. Below are some examples of these religious math applications.

Constructing religious objects

Image: Śrauta ritual (Photo: Srkris, Public Domain)

The Śulba Sūtras are ancient Indian texts that provide instructions for ritualistic practices in Vedic religion. Specifically, the Śulba Sūtras focus on geometry and measurements related to constructing altars for religious ceremonies. The mathematical applications discussed in the Śulba Sūtras include methods for constructing altars of different shapes that occupy the same area.

Some scholars even argue that these religious needs paved the way for the development of mathematics in ancient India, suggesting that the Babylonians later acquired their mathematical knowledge from Indian sources.

Astrology and Numerology

Image: Astrology chart

In ancient Hellenic societies, mathematics served practical needs like counting and measuring, as well as mystical purposes, such as rituals aimed at interpreting the will of the gods. One of the most common examples is astrology, where mathematical calculations of planetary positions and movements supported the belief that celestial bodies influence human affairs. Another example is numerology, where numbers were assigned mystical significance, often attributing spiritual meanings to numerical values.

Planning religious festivals

Image: Mesopotamian God of agriculture, hunting, and war (Image: Katolophyromai – Own work, CC0)

Specific examples of these math applications include the solar and lunar calendars of the Babylonians, which were based on detailed observations of the moon and sun. These calendars not only served practical needs, such as agricultural planning, but were also used for scheduling religious festivals. For instance, the Babylonian New Year festival, known as Akitu, was celebrated in spring and marked the rebirth of nature. It was a time for rituals to honor the gods and ensure fertility and prosperity for the coming year.

Moreover, the Babylonians divided the year into months that were aligned with lunar phases, allowing them to predict the timing of key agricultural activities and religious observances. This careful planning demonstrated the deep connection between mathematics, astronomy, and religious practices in their society.

Political aspects of math applications

Public counting for transparency and democracy

In the early days of democracy, math played a role in ensuring fairness and transparency. Citizens’ understanding of basic math helped ensure that political decisions served the public interest. For example, in classical Athens, public records of financial operations were displayed for citizens to review, promoting transparency and allowing scrutiny of how resources were used. The city maintained detailed accounts of financial activities, and officials were required to report them. Any citizen could be called upon to verify calculations or perform sums for the benefit of the city [24].

Conclusion:

Having reviewed the history and development of mathematical applications, we can draw several key conclusions about the enduring role of math in society.

Conclusion 1: Math Serving Basic Needs
Mathematics has consistently supported society’s basic needs, both physical and cultural, across thousands of years—from food production and construction to navigation, transportation, and entertainment. Over time, math applications have evolved to relieve people of physical labor and repetitive tasks. This trend continues today, as math increasingly helps streamline and ease everyday activities. As history suggests, this pattern is likely to remain in place, with math continuing to support essential human needs into the future.

Conclusion 2: Fundamental Math Stays the Same
Despite technological advances, the fundamental principles of math often remain unchanged. For instance, the principles of triangle geometry have been key to navigation for millennia. In ancient times, navigation relied on simple geometric properties (e.g., Thales’ ship problem ↑), then advanced to trigonometry. Today, even complex systems like GPS rely on triangle-based methods, such as trilateration. This enduring reliance on foundational math concepts, like those in trigonometry, highlights why learning these basics remains relevant, even in a high-tech world.

Conclusion 3: Math Reaches Every Part of Life
Finally, math applications have become pervasive, extending into new areas of life as technology advances. One example is medicine, where math was once rarely involved but now plays a major role, especially with the development of advanced medical devices. For example, mechatronic rehabilitation devices use mathematical principles like the Pythagorean theorem for precision ↑. As technology progresses, math will likely continue to find new applications across various fields, deepening its impact on daily life.

References:

Pollak, H. O. (1970). Chapter VIII: Applications of Mathematics. Teachers College Record, 71(5), 311-334. https://doi.org/10.1177/016146817007100508
Vos, Pauline. ““How real people really need mathematics in the real world”—Authenticity in mathematics education.” Education Sciences4 (2018): 195.
Boaler, J. (1993). The Role of Contexts in the Mathematics Classroom: Do They Make Mathematics More “Real”? For the Learning of Mathematics, 13(2), 12–17. http://www.jstor.org/stable/40248079
Jansen, B. R., Schmitz, E. A., & Van der Maas, H. L. (2016). Affective and motivational factors mediate the relation between math skills and use of math in everyday life. Frontiers in psychology, 7, 513.
Mosvold, R. (2005). Mathematics in every day life a study of belief sandactions. Unpublished doktoral dissertion), Department of Mathematics University of Bergen, Norveç.
Glazer, E., & McConnell, J. W. (2002). Real-life math: Everyday use of mathematical concepts. Westport, CT: Greenwood Press.
Classen, M. (2002). Applying math to real life. School Libraries in Canada, 22(1), 30.
Lovell, R. S. (2016). Real-World Applications in Math Class.
Yavuz Mumcu, H. (2018). Examining Mathematics Department Students’ Views on the Use of Mathematics in Daily Life. International Online Journal of Education and Teaching, 5(1), 61-80.
Robson, E. (2009). Mathematics, metrology, and professional numeracy. In The Babylonian World(pp. 428-441). Routledge.
Tiede, V. (2020, December). Ziggurats: An Astro-Archaeological Analysis. In Harmony and Symmetry. Celestial regularities shaping human culture.: Proceedings of the SEAC 2018 Conference in Graz. Edited by Sonja Draxler, Max E. Lippitsch & Gudrun Wolfschmidt. SEAC Publications; Vol. 01(Vol. 1). tredition.
Scriba, C. J., & Schreiber, P. (2015). 5000 years of geometry: Mathematics in history and culture. Birkhäuser.
Michel, C. (2010). Writing, counting and scribal education in Aššur and Kaniš. Anatolia’s Prologue Kültepe Kanesh Karum. Assyrians in Istanbul, 82-93.
Bloch, Y. (2014). Judeans in Sippar and Susa during the first century of the Babylonian Exile: assimilation and perseverance under Neo-Babylonian and Achaemenid Rule. Journal of Ancient Near Eastern History, 1(2), 119-172.
Historical-Mathematical Studies, edited by G. F. Rybkin and A. P. Yushkevich. — Volume X. — Moscow: GITTL, 1957. — 820 pages.
Dahan-Dalmedico, A., & Peiffer, J. (1986). Une histoire des mathématiques: Routes et dédales. (No Title).
Physical and Mathematical Sciences in Eastern Countries: Collection of Articles and Publications. Volume I (IV). — Moscow: Nauka, 1966. — 359 pages.
Bozik, M. S., & Ustaoğlu, M. (2020). The merchant societies and usury: Assyrians and Babylonians. In A History of Interest and Debt(pp. 35-46). Routledge.
Berezkina, E. I. Mathematics of Ancient China. — Moscow: Nauka, 1980.
Raik, A. E. Essays on the History of Mathematics in Antiquity. 2nd ed., revised and expanded. — Saransk: Mordovian Book Publishing House, 1977. — 370 p.
Roth, J. (1995). The length of the siege of Masada. Scripta Classica Israelica, 14, 87.
Historical and Mathematical Studies, edited by G. F. Rybkin and A. P. Yushkevich. — Volume XI. — Moscow: GITTL, 1958. — 793 p.
Matvieva, G. P. The Development of Plane and Spherical Trigonometry: (From the History of Mathematical Ideas). — Moscow: Knowledge, 1982. — 64 p. — (New in Life, Science, Technology. Mathematics, Cybernetics; 5/1982).
Cuomo, S. (2005). Ancient mathematics. Routledge.
Customs and Traditions of the Canadian Military Engineers (the “Red Book”), A-JS-007-003/JD-001
Theory and Practice in Heron’s Mechanics Schiefsky, Mark J. 2007