Trigonometry in Robotics
Introduction:
Observe the brief animation below, illustrating the motion of a robotic hand.

Take note of the remarkable precision in the robot’s movements. This precision is the result of intricate mathematical calculations. Trigonometry stands out as a crucial mathematical concept extensively employed in the field of robotics. In the following sections, we’ll delve into an example showcasing how robots utilize trigonometry to navigate right triangles, exploring how these calculations aid in determining missing sides, contributing to the exceptional accuracy of robotic movements.
Example: The Drilling Robot
Examine the drilling robot featured below. To ensure precise accuracy, the robot must consistently determine the current position of the drill point. But how is the position of the drill point calculated?
Firstly, let’s represent each moving section of the robot as a straight line, effectively constructing the mathematical model of the robot:

Next, consider each line as a hypotenuse and construct a series of right triangles:
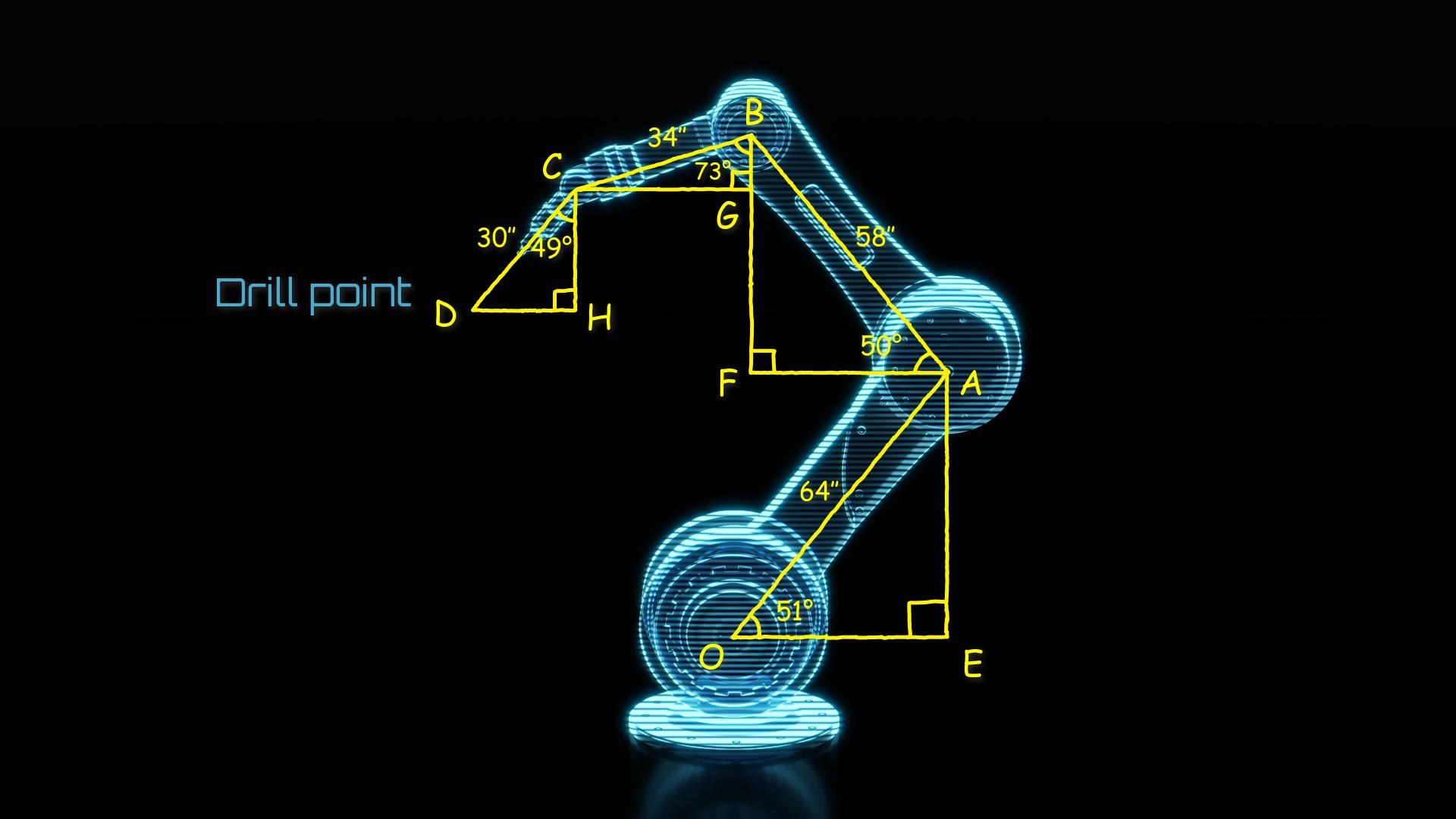
Point D corresponds to the drill point. Let’s find the x-coordinate of this point. This can be achieved by adding and subtracting values of the “horizontal” legs:
\[X = 0 + OE – AF – CG – DH\]
We are aware of the length of each hypotenuse (defined by the robot’s dimensions) and the values of the two angles connected to a hypotenuse (determined by special sensors attached to the robotic arm). This implies that for each triangle, we possess the hypotenuse and all angles, which is adequate to determine a missing side in each triangle using trigonometry.
Detailed Calculation:
Let’s delve into the detailed calculations:
OE is the side adjacent to the angle AOE, which is 51°. Therefore:
\[\small OE = 64″ \times \cos(51°) = 40.28″\]
Using the same approach, we can determine AF, CG, and DH:
\[\small AF = 58″ \times \cos(50°) = 37.28″\]
\[\small CG = 34″ \times \sin(73°) = 32.51″\]
\[\small DH = 30″ \times \sin(49°) = 22.64″\]
Now, we can find the x-coordinate:
\[\scriptsize 40.28″ – 37.28″ – 32.51″ – 22.64″ = -52.15″\]
Thus, by determining the lengths of the “horizontal” sides in our triangles, we successfully found the x-coordinate. The y-coordinate can be found in a very similar way (i.e., by determining the lengths of the “vertical” sides of the triangles).
Conclusion:
In summary, you’ve witnessed how the robotic arm can be effectively modeled using a set of right triangles. Through this model, we can determine the missing sides of these triangles and subsequently calculate necessary coordinates using trigonometry. This example vividly demonstrates the power of mathematics – breaking down a real-world object (a robotic arm) into small mathematical components (right triangles) and employing well-established mathematical principles (finding missing sides of right triangles) to address a real-life challenge (ensuring precision in the robotic arm).
References:
Ensure that the example we’ve discussed above is indeed real!
- Did you know that the International Space Station (ISS) robotic arm (Canadarm2) operates with the help of trigonometry? From Wikipedia:
“The Canadarm2 robotic manipulator on the International Space Station is operated by controlling the angles of its joints. Calculating the final position of the astronaut at the end of the arm requires repeated use of trigonometric functions of those angles.”

By NASA – Public Domain, Link
Now you understand the fundamental principle of how such control can be achieved!
Video Version
We’ve also prepared a video version of this article. It provides an easy-to-follow, animated explanation of the example and contains more in-depth information, such as finding the y-coordinate of the robotic arm by determining the missing “vertical” sides of triangles. Check the free preview below or subscribe to get access to our full videos.
Further Reading:
For those who want to delve deeper, we have other related articles. If you are interested in additional applications of trigonometry, feel free to explore our article about using trigonometry in the oil & gas industry:
For those keen on understanding more about how mathematics is employed to ensure precision in robots, check out our article about medical mechatronics:
