The 3-4-5 Triangle: A Real-Life Example (from Mechatronics)

The 3-4-5 triangle, a famous Pythagorean triple, finds use in construction, DIY projects, and even in Internet technologies. This article explores another example of the 3-4-5 triangle's application – in medical mechatronics.

• Published: November 1, 2023

• Last update: October 30, 2024

• Grades: 8th and older

The 3-4-5 Triangle in Mechatronics

Introduction: What is Mechatronics?

Mechatronics is a blend of various technologies that empower the creation of highly advanced products, including robots, smart machines like vending machines, and automated systems such as car automatic gearboxes. The term “mechatronics” itself combines “mechanics” and “electronics.” Initially, mechatronics involved the integration of mechanics and electronics, with electronic devices controlling mechanical components. Over time, mechatronics has expanded to encompass not only mechanics and electronics but also specialized software, telecommunications, smart cameras, and other cutting-edge technologies.

Medical Mechatronics

Mechatronics plays a crucial role in healthcare, enabling the creation of advanced surgical robots, prostheses, and even exoskeletons. An exoskeleton is an external frame that aids the human body in performing various tasks, such as rehabilitation after a traumatic injury. The following section will explain how the 3-4-5 triangle is involved in the operation of exoskeletons.

Constructing a 3-4-5 Triangle in Exoskeletons: an Example

The figure below displays an x-ray image of one joint of the exoskeleton, known as a scissors linkage or scissors mechanism.

Despite its apparent complexity, this system elegantly employs the Pythagorean theorem. Let’s explore an example.

Consider a simple model: moving a platform attached to a linkage upwards, as shown in the animation below:

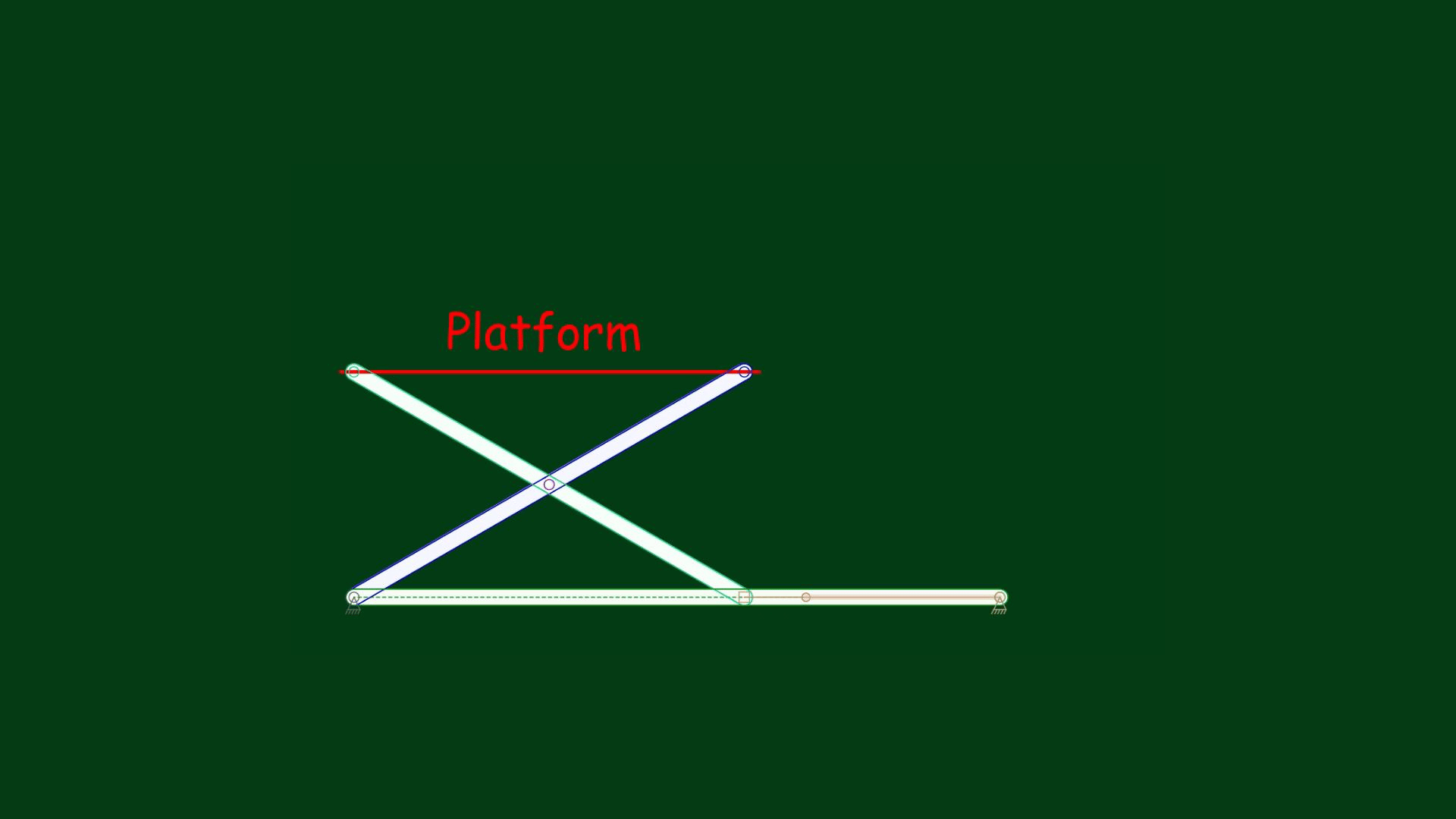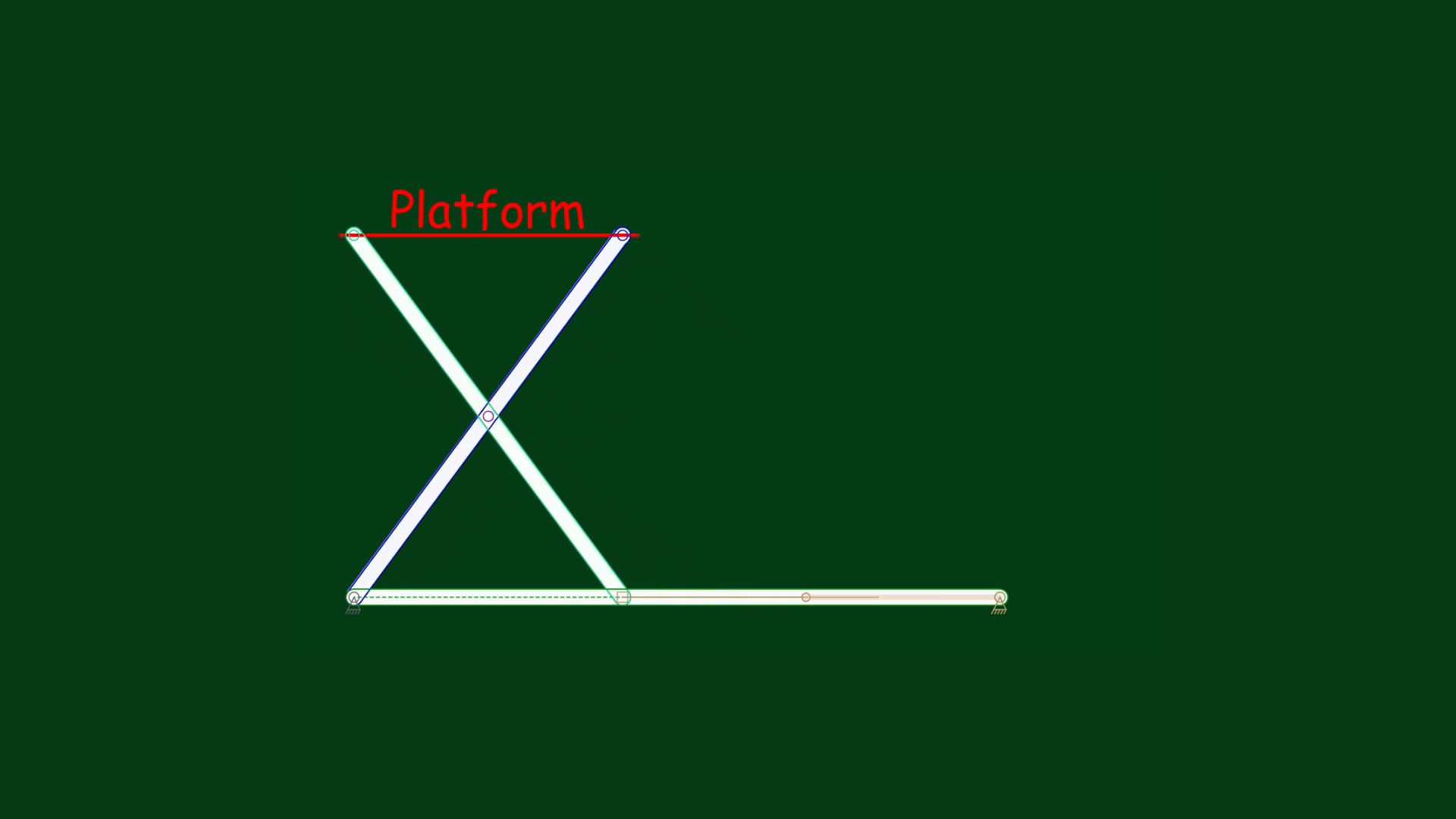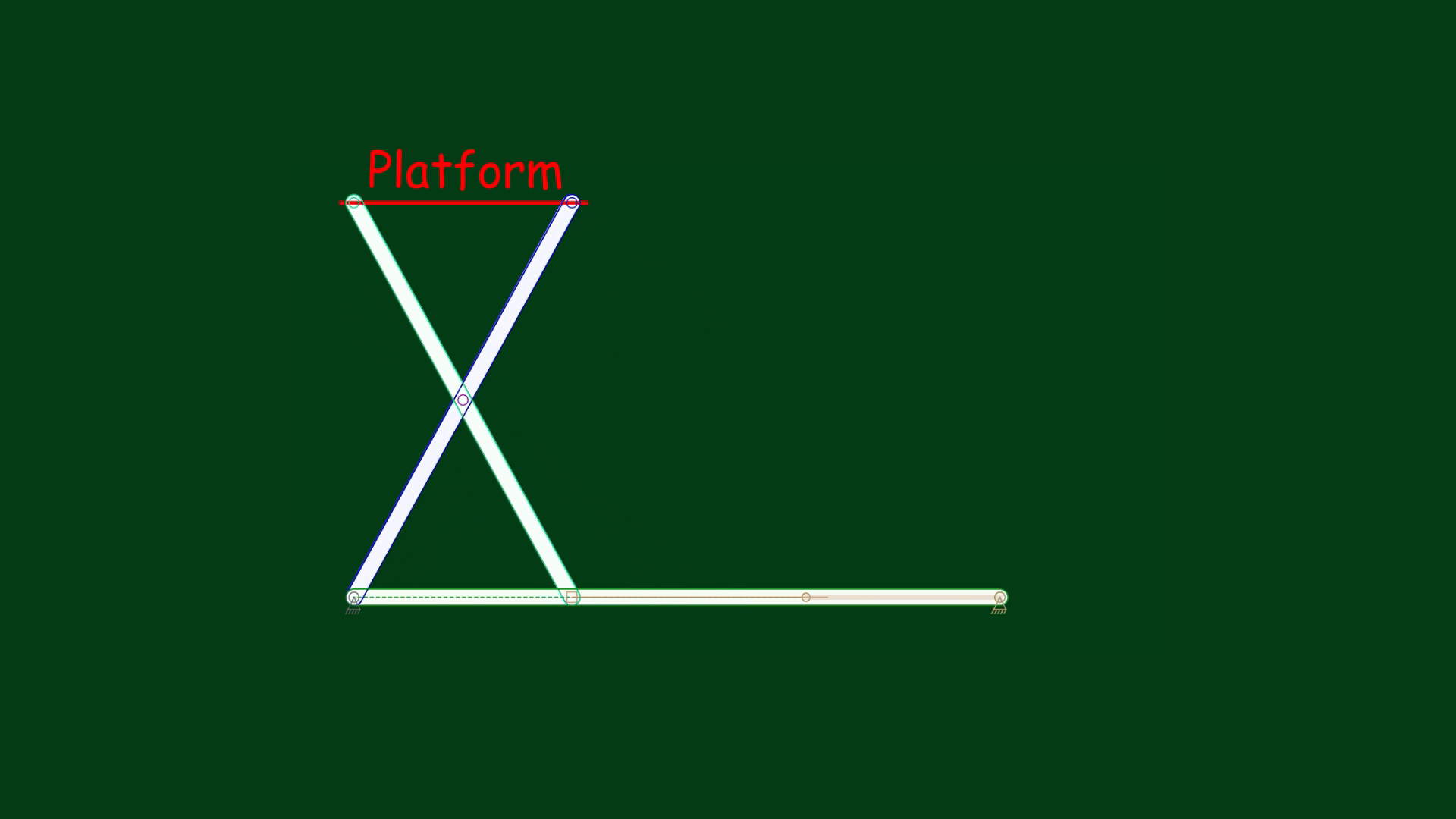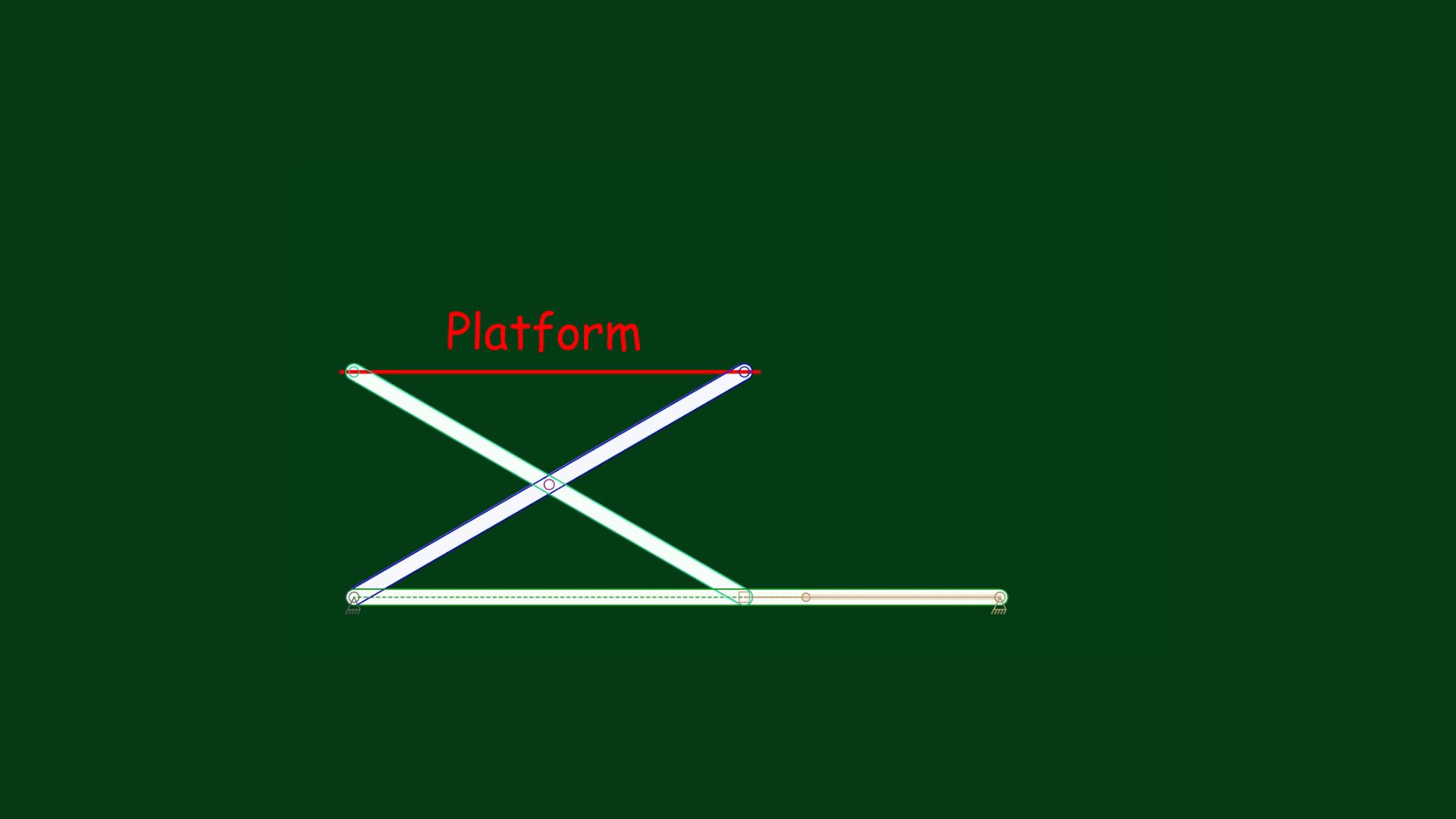
Suppose we need to move the platform to a specific height, say, 4 inches. Perhaps you have already noticed that this mechanism can be modeled using a right triangle – and therefore, the Pythagorean theorem can guide this process.

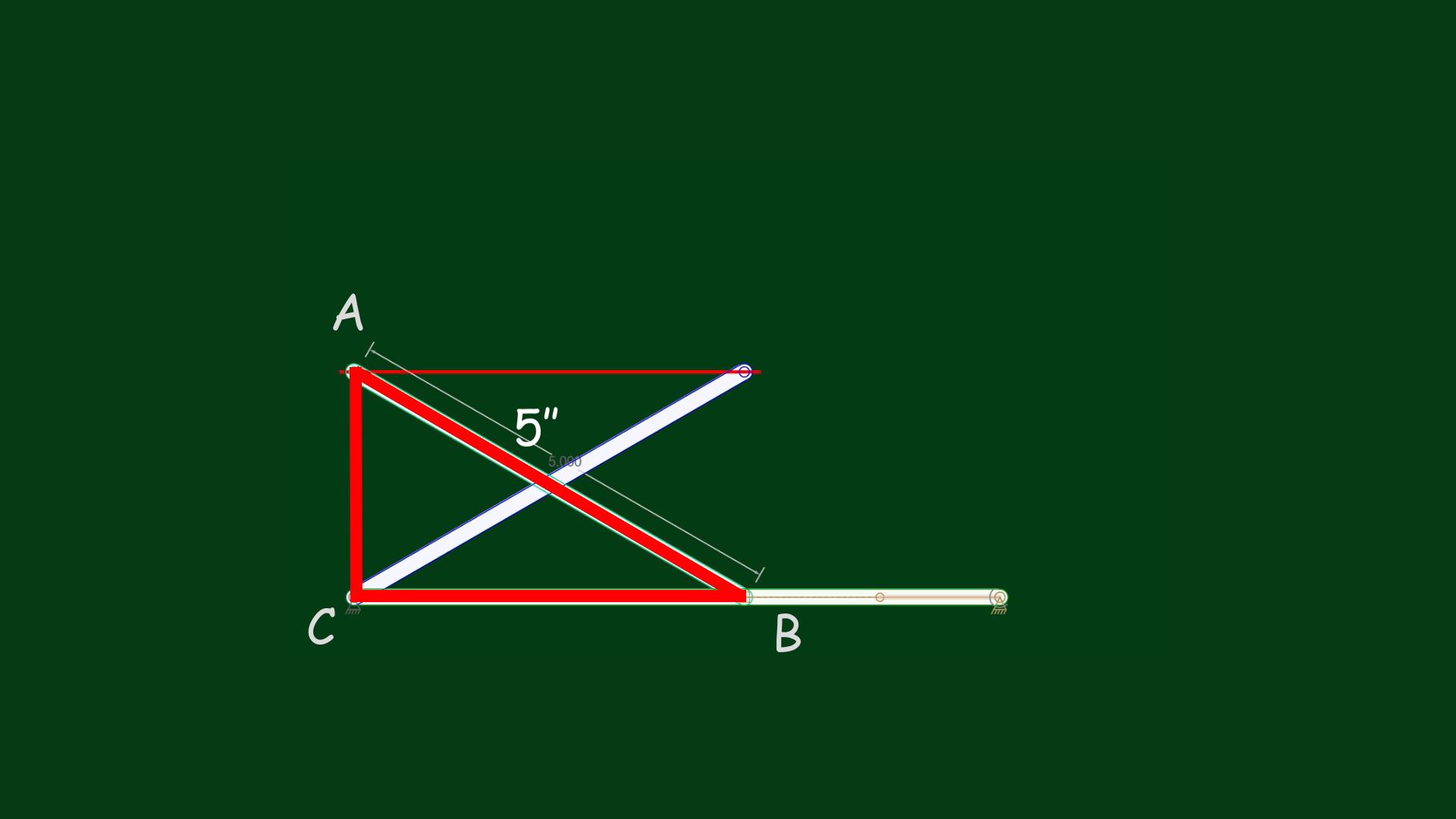
Let’s draw a right triangle model (ABC). Moving the platform up means that the point B must be pushed to the left. Let the hypotenuse AB be 5 inches long. A platform height of 4 inches means that the leg AC must be 4 inches long. If one leg of the right triangle is 4 inches long and the hypotenuse is 5 inches long, then we have a 3-4-5 triangle model. Applying this, we know that the length of the leg BC must be 3 inches. Let’s check it in the animation below:

Indeed, the animation has shown that the platform has moved exactly to a height of 4 inches, and the model of the scissors linkage became the scalene 3-4-5 triangle, according to the Pythagorean theorem:

\[ \sqrt{5^2 – 4^2} = 3 \]

Applying the theorem allows for moving the platform up and down with very high accuracy – something crucial in mechatronics.

Conclusion:

While the Pythagorean theorem may seem like a simple concept, such seemingly straightforward mathematical principles are frequently employed in the development of highly technological products, allowing engineers to achieve remarkable precision and accuracy. It’s important to remember that the 3-4-5 triangle is just one specific example of the Pythagorean theorem in action.

References:

We utilized a set of publications about the development of medical prostheses and exoskeletons while preparing this article:

Video version

The animated video version of this article provides more examples and delves deeper, offering specifics on how the linkage works and how travel distances are calculated. It brings the information even closer to real-world settings. Check the preview below or subscribe to get access to our full videos.