Calculating the Value of cosx in Petroleum Engineering
Introduction
A large portion of the energy we consume still comes from hydrocarbons, like oil or natural gas. Different specialists in the oil and gas industry are involved in the exploration, production, transportation, and processing of these hydrocarbons. The following illustrates a situation where the calculation of the cosine value is a crucial part of their work.
Drilling an Oil Well
Oil production involves the drilling of oil wells. As depicted in the figure below, oil wells can be vertical, inclined, and even horizontal, reaching depths of several thousand feet.
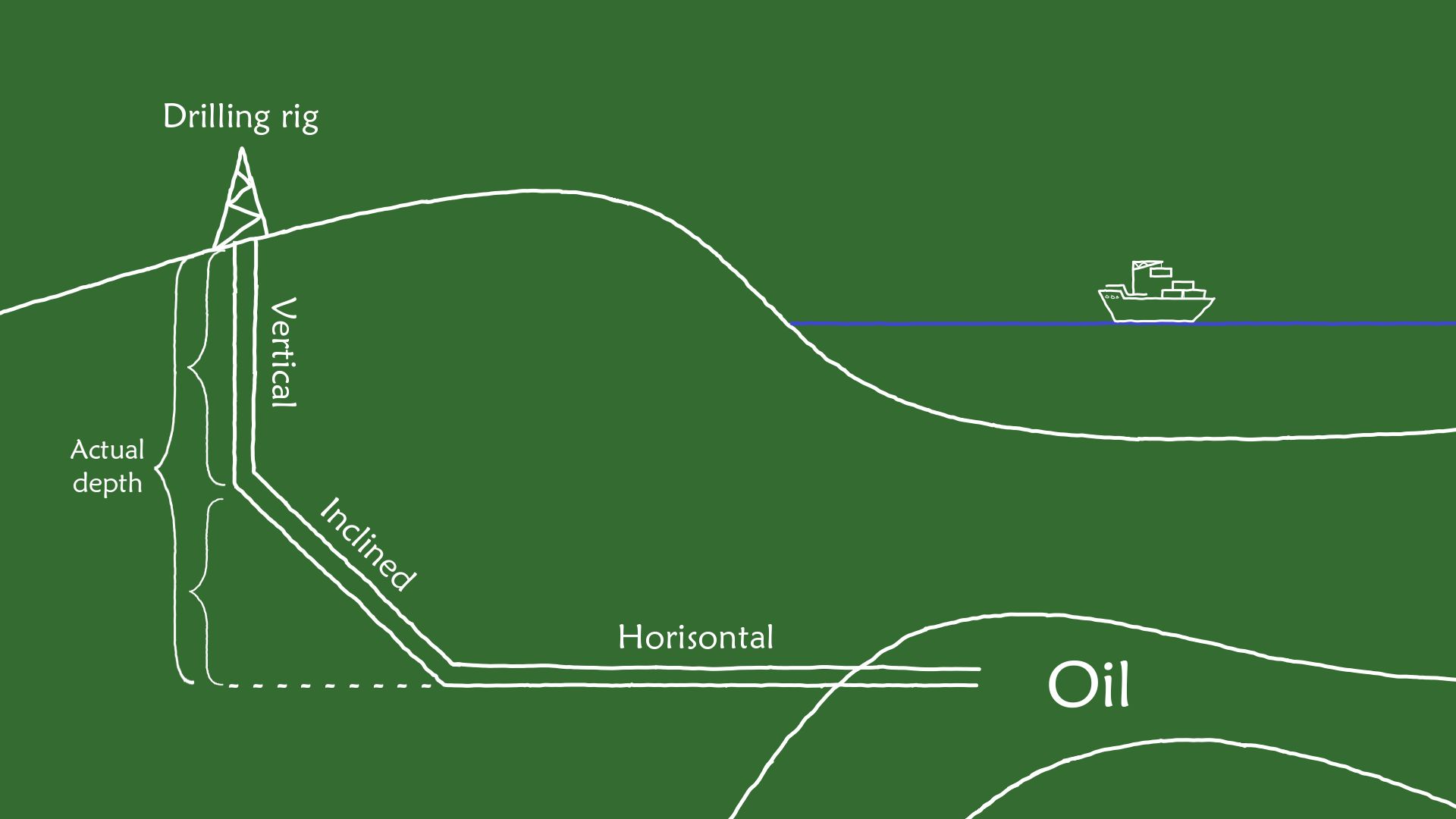
During the drilling process, it becomes crucial to measure the actual depth (called True Vertical Depth) of the drill bit at various stages. Calculating the depth of a vertical oil well is straightforward. However, determining the true vertical depth of an inclined oil well presents a challenge. This is where the knowledge of cosx becomes very useful.
Calculation Example:
How They Determine the Value of an Angle for cosx?
Take a look at the animated drilling of the oil well below.

Initially, it was drilled vertically to a depth of 30 feet. Subsequently, the inclination angle was changed by 20 degrees, and another 30 feet were drilled. To determine the actual depth of the oil well, oil and gas specialists create a right triangle model and use trigonometry for calculation.
To determine the true vertical depth of the oil well, oil and gas specialists create a right triangle model and employ trigonometry for calculation.
The actual depth consists of the vertical part and the adjacent leg of a right triangle shown in the animation above.
We know that:
\(\cos{x} = \frac{\text{adjacent leg}}{\text{hypotenuse}}\).
Therefore, transforming this formula gives us:
\[
\small
\text{adjacent leg} = \cos{x} \times \text{hypotenuse}.
\]
The hypotenuse of this right triangle is 30 feet long, and the adjacent angle measures 20 degrees. Then:
\[ \cos{x} = \cos{20^\circ} \approx 0.94 \]
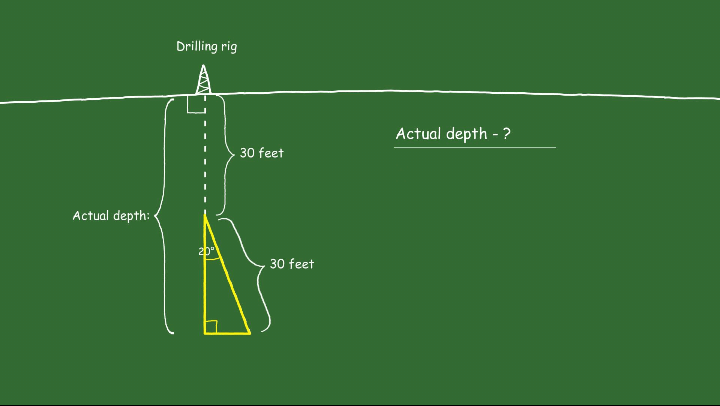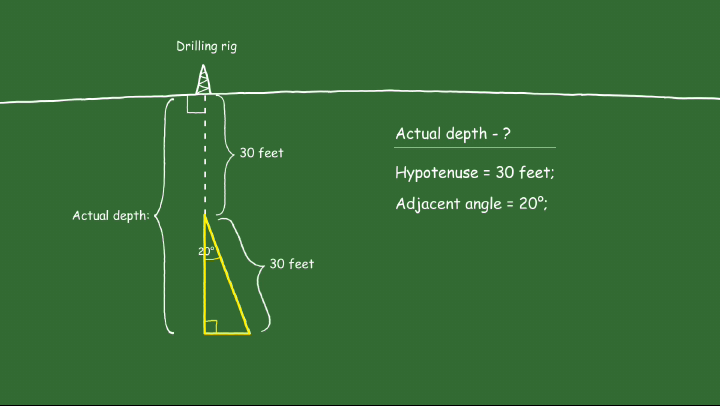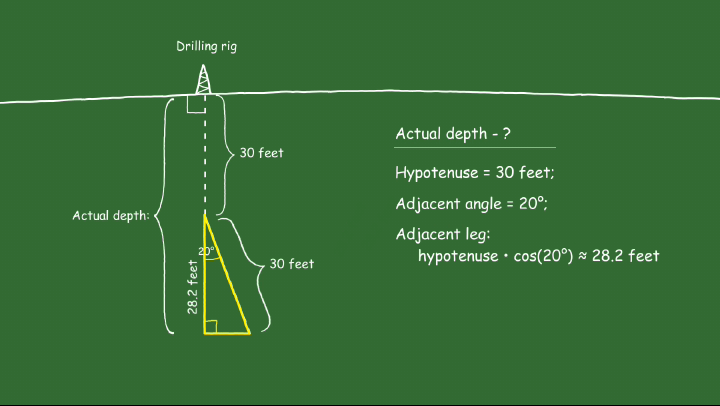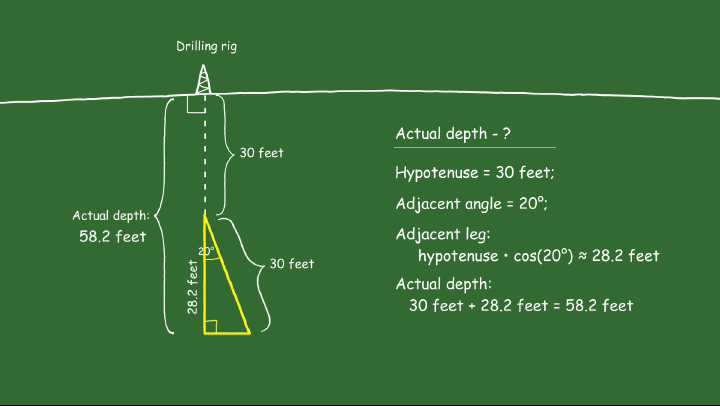
Using this information, we can find the length of the adjacent leg of the triangle:
\[ 30 \times 0.94 = 28.2 \, \text{(feet)} \]
Now, to find the actual depth of the oil well:
\[ 30 + 28.2 = 58.2 \, \text{(feet)} \]
Therefore, the actual depth of this oil well is 58.2 feet. These calculations are shown in the animation below.
Today, drill bits are “smart” and equipped with special inclination sensors that transmit information about both the inclination angle and azimuthal angle.
Conclusion:
As you have seen, understanding what cosx is and knowing how to calculate it is incredibly useful. Just imagine standing on the ground and having the precise knowledge of where the drill bit is! This showcases the power of mathematics—often enabling the calculation of coordinates for physical objects (like a drill bit) when they are not visible or manually measurable.
Similar methods of calculating sines and cosines, as demonstrated here, are also applied in various fields such as space, robotics, medicine, and more.
References:
For preparing this article, we utilized various sources. One of them is:
Feel free to check Chapter 7 in the preview of this book to understand the significance of trigonometry for oil and gas specialists.
Additionally, you might be interested in watching a video (created by the K20 Center for Educational and Community Renewal at the University of Oklahoma) in which a drilling engineer discusses the application of math and trigonometry in the work of oil and gas specialists:
Video version
The video version of this article delves deeper, offering not only animated and user-friendly explanations but also demonstrating the calculation of both cosx and sinx in oil well drilling. Enjoy the preview below, or subscribe to gain access to our complete video library.
Further Reading:
For those interested in further exploration, we offer other related articles. If you wish to discover additional applications of trigonometry, feel free to explore our article on using trigonometry in robotics:
