Area of Composite Figures in Water Supply and Management
Introduction
Water management is the careful protection of our water resources, encompassing drinking water, non-potable water, wastewater, and stormwater. This intricate process aims to ensure the sustainable and equitable utilization of this precious resource. As our population grows and climate change intensifies, effective water management becomes increasingly vital. This growing importance is why careers in water resource management are expected to be in high demand in the future.
Measuring Water Flow Rate
The first step in water management involves collecting water. Specialists monitor natural basins to understand their condition. What does monitoring involve? Monitoring goes beyond just looking; it includes various measurements, like figuring out how fast water flows in rivers or streams. Measuring water flow rate is crucial as it helps specialists notice changes in basin condition. The Velocity-Area method is commonly used. In this method, specialists calculate the cross-sectional area of the river or stream by multiplying it by the flow’s velocity. The cross-sectional area, often a composite figure, requires knowledge of how to calculate its area. A detailed example follows.
Example:
Imagine a water canal represented by the cross-sectional area in the figure below, with water flowing at a speed of 2.3 ft/s.
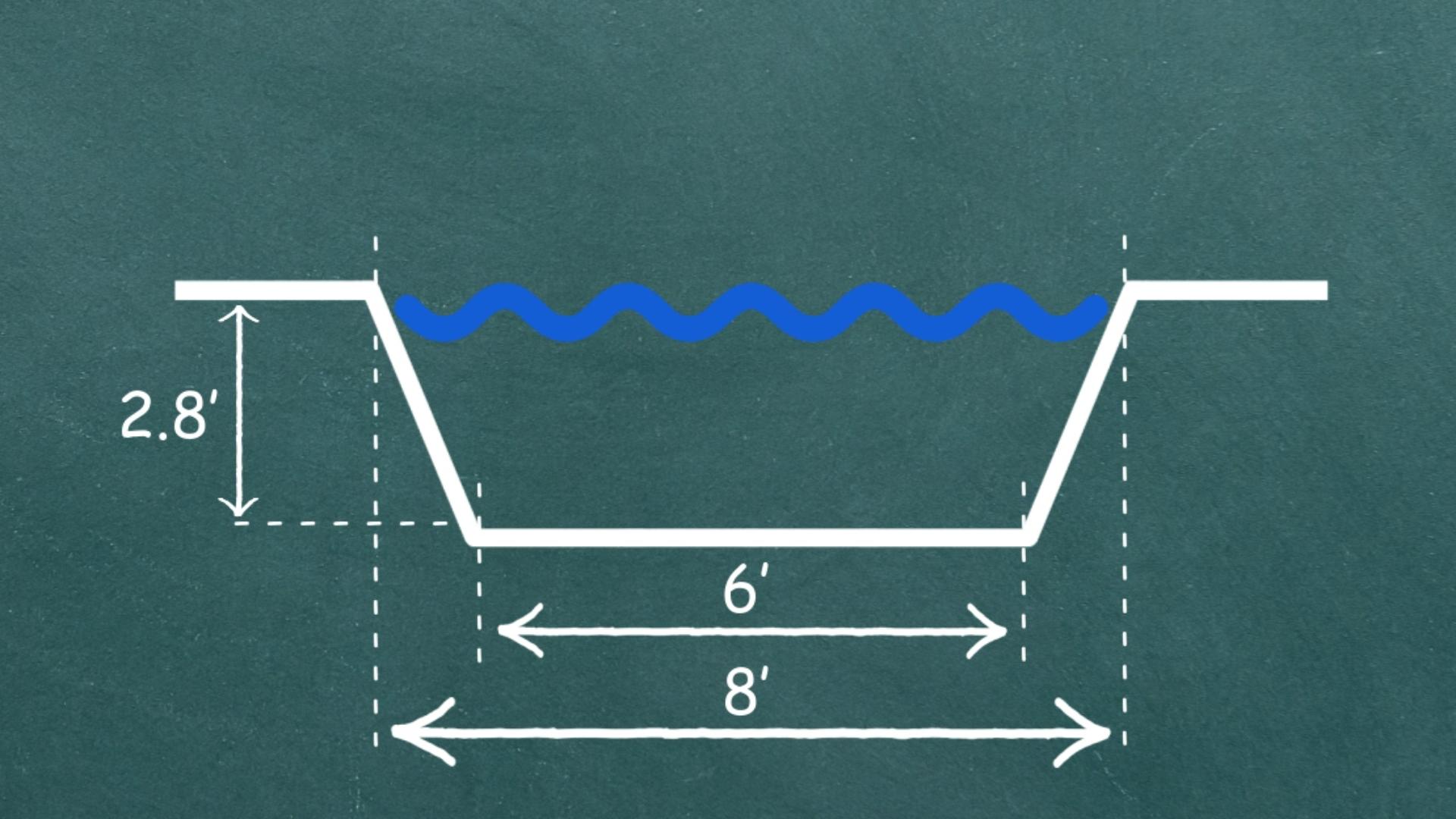
The canal’s cross-section is a composite figure, made up of a rectangle and two triangles, as illustrated in the animation below.
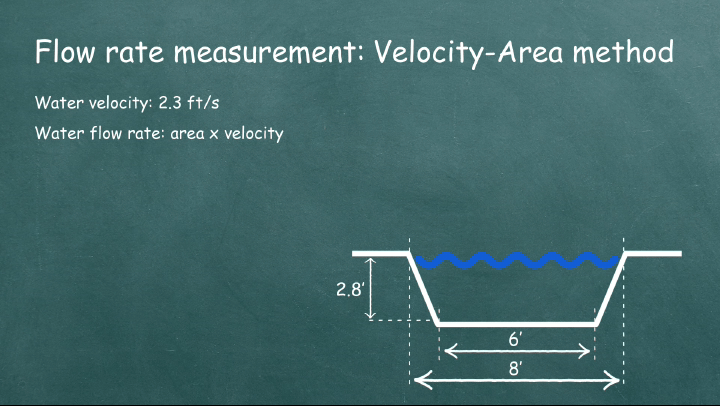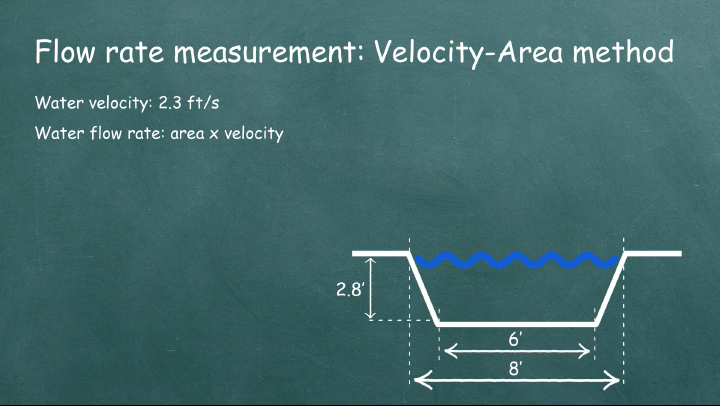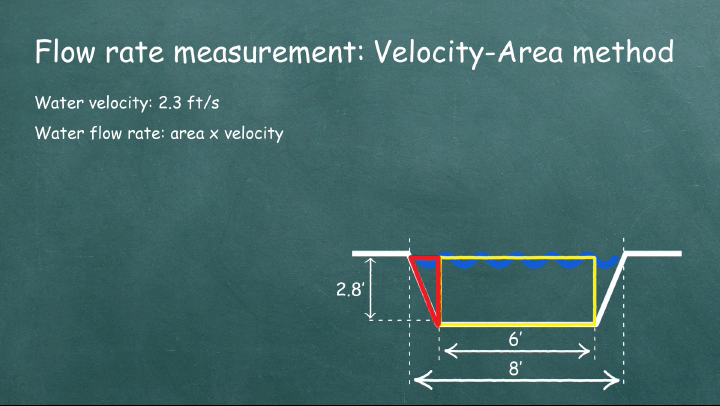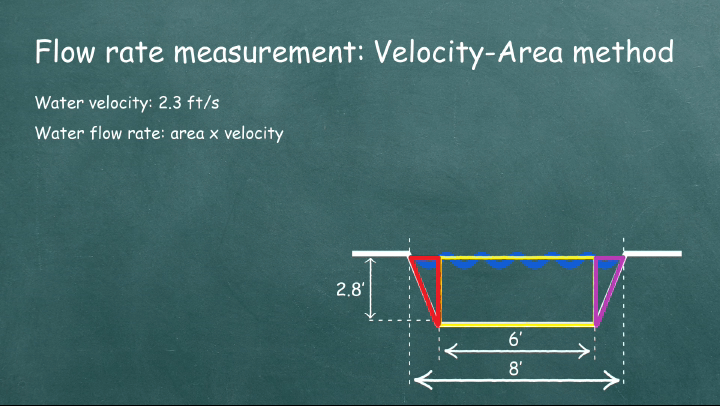
The area of the rectangle is calculated as:
\(6” \times 2.8” = 16.8 \, \text{ft}^2\).
Each triangle’s area is calculated using:
\(\frac{1 \times 2.8}{2} = 1.4 \, \text{ft}^2\).
By adding these areas, we find the total cross-sectional area of the canal:
\(16.8 + 2 \times 1.4 = 19.6 \, \text{ft}^2\).
This is the area of the composite figure, representing the canal’s cross-section. Using this data, we can determine the water flow rate, which is:
\(19.6 \times 2.3 = 45.1 \, \text{ft}^3/\text{s}\).
Conclusion:
The world around us may seem complex, and mathematics might feel distant from real life. However, complex things can often be broken down into simple parts. In this case, the composite figure of the cross-section of the canal can be simplified into two basic figures: a rectangle and triangles. Once simplified, performing the necessary calculations becomes much easier, as demonstrated in this example.
References:
For the reliability and authenticity of the information presented, we’ve consulted the following sources:
- “Math for Water Treatment Operators” by J. Giorgi (2011). This book, specifically Chapter 4 “Water Treatment” (page 213), covers flow and velocity problems, resembling the tasks discussed in this article.
- Water Treatment and Distribution Operator Math Reference Sheet by the American Water Works Association. This resource provides formulas for calculating areas of figures and flow rates.
- Additional insights into the velocity-area method were obtained from descriptions available on Elsevier ScienceDirect.
- Finally, in a video by American Water College, the tutor explains the calculation of flow rates using the velocity-area method, mirroring the approach detailed in this article:
These references collectively contribute to the reliability and authenticity of the information shared in this article.
Video Version
Explore the dynamic world of water management specialists through the video version of this article!
This content delves deeper into their work, illustrating how they calculate the area of composite figures to fulfill their professional responsibilities. The video breaks down the calculations presented in this article in an easy-to-follow animated format. Beyond mathematics, it provides insights into the roles of other subjects such as chemistry and biology in the realm of water management specialists.
Preview the video below or subscribe to access our complete collection.
Further reading:
We also have other blog articles that explain the importance of understanding properties of composite figures in real life. Check out more:
