Circumference Formula in Microbiology
Introduction
So, you’ve learned the formula: \[c = 2 \pi r\] and have been working on exercises in your textbook. But why are these exercises useful? Where might you need the skill of calculating circumference?
In reality, these skills come in handy in many unexpected situations, like in microbiology. At first glance, you might think that microbiology and math don’t have much in common. However, that’s not entirely true. Next paragraphs will explain why.
How to Measure Bacteria Growth?
Microbiologists often observe bacteria growth, which involves measuring and documenting the growth of bacteria over time. Circle math, specifically the knowledge of circumference, is widely used for these measurements.
Consider the E.coli bacterium, a rod-shaped microorganism measuring approximately 2 microns long and 0.4 microns wide:
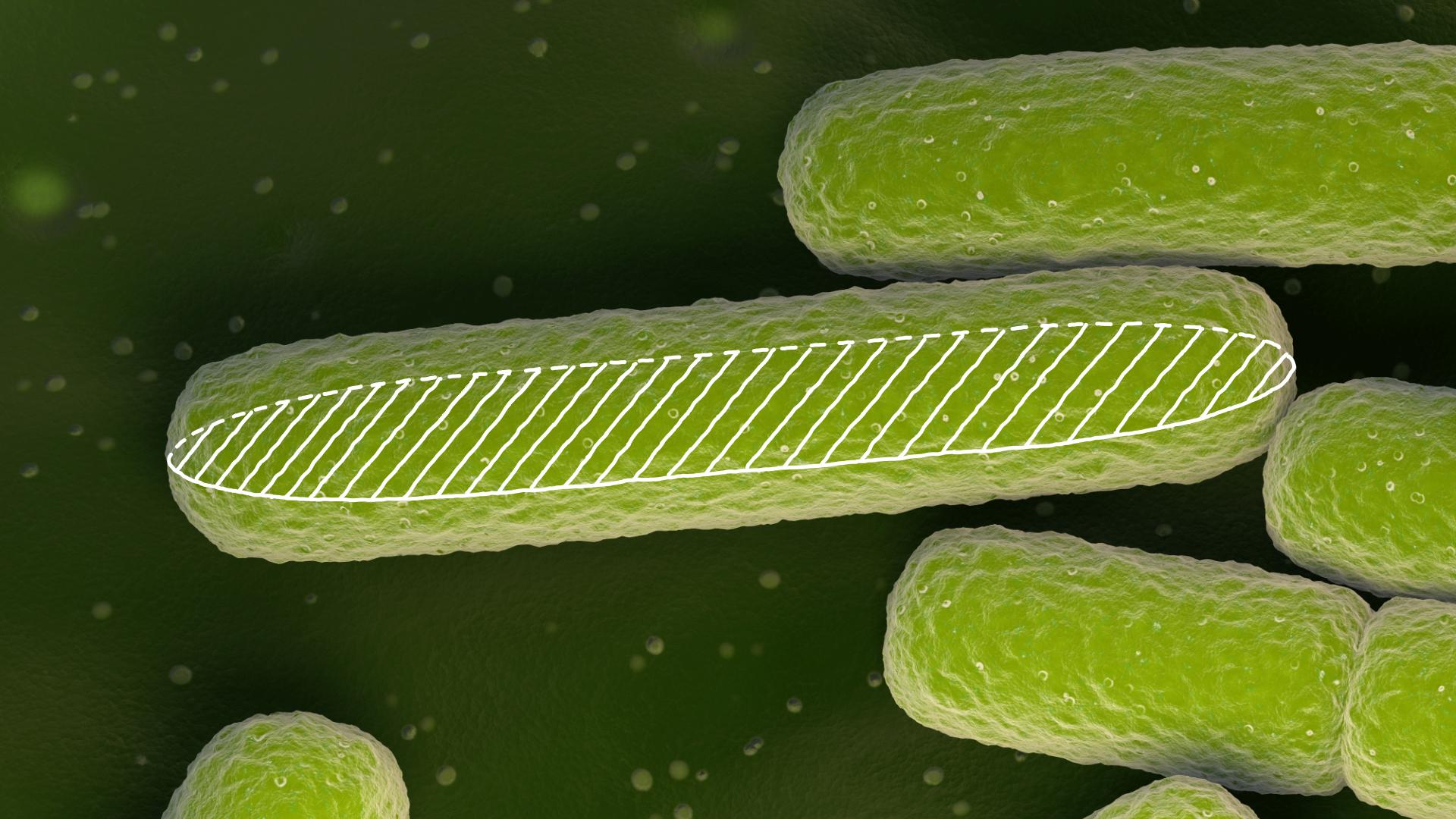
The dashed area on the picture represents the transverse section of this bacterium. As the bacterium grows, the perimeter of the transverse section gets longer. Measuring the perimeter helps understand how much the bacteria has grown.
Calculation:
Suppose we have a bacterium that is 2 microns long and 0.4 microns wide. The transverse section of this bacterium is a composite shape, which can be divided into a rectangle and two semicircles. To calculate the perimeter, add half of the circumference length, the long side of the rectangle, half of the circumference length again, and the long side of the rectangle. This is illustrated in the animation below:
If the width of the bacterium is 0.4 microns, the radius of the semicircle is 0.2 microns. The length of the semicircle is then:
\(\frac{2\pi R}{2} = \pi \times 0.2 \approx 0.63 \, \text{microns}\)
If the length of the bacterium is 2 microns, then the long side of the rectangle equals 1.6 microns (length of the bacterium minus two radii of the semicircle).
Finally, the perimeter of the transverse section of the bacterium equals:
\(2 \times 0.63 + 2 \times 1.6 = 4.46\) microns.
As the bacteria grows, microbiologists repeat this measurement procedure and document changes in the length of the perimeter.
Why is Measuring Bacteria Growth Needed?
Measuring the growth of bacteria serves various important purposes. One significant example is in the development of new drugs that target bacteria. When bacteria are exposed to these new drugs, measuring their growth becomes crucial in understanding whether the drug is slowing down their growth.
Conclusion:
As you’ve seen, knowledge of middle-school math, like the circumference formula, is incredibly useful in advanced fields such as microbiology. Importantly, it’s not limited to just microbiology; this formula finds applications in various other professions like construction engineering, carpentry, architecture, landscape design, and more. Knowing math proves beneficial in many aspects of life!
Check the Facts!
It’s always a good idea to verify information. You can confirm the validity of the described method in scientific publications. The reference we used for this article is:
Video version
Further reading:
Interested in how the concept of circumference is useful in other real-world situations? Check out the article “How to Find a Central Angle: A Real-Life Example (from Civil Engineering)” to understand how circumference and the central angle of a circle are used in designing and building roadways.
If you’re interested in seeing how calculating the area of composite figures is used in other real-world domains, you’re welcome to explore an example from the water supply domain: Area of Composite Figures: A Real-life Example (from Water Supply).