Piecewise Linear Function for Analyzing Public Health Data
What is Public Health?
Public health involves various government efforts to ensure the well-being and safety of everyone. It encompasses the promotion of hygiene, vaccination, prevention of drug usage, encouragement of a healthy lifestyle, advocacy for sustainable nutrition, and the prevention of depression, among other things. The goal is to maintain the health and happiness of our entire community.
Who Are Public Health Specialists?
The work of public health specialists is incredibly diverse, involving professionals in various roles. Some specialists focus on analytics and forecasting, using mathematics to predict and manage collective PTSD. One widely-used mathematical concept for such forecasting is the piecewise linear function. The following section will delve into more details.
What is PTSD?
PTSD stands for Post-Traumatic Stress Disorder, a psychiatric condition that may develop after experiencing a traumatic event like war, earthquakes, or similar incidents. It can also affect a group of individuals who have shared traumatic experiences, such as a terrorist attack. Effective public health systems should be able to predict the emergence of collective PTSD and respond appropriately.
Using Piecewise Linear Function to Predict PTSD: An Example
Take a look at the graph presented below.

This graph, plotted on a Cartesian coordinate plane, illustrates the evolution of stress levels over time for two age groups that have experienced a terrorist attack. The x-axis represents time elapsed since the attack, while the y-axis represents the stress level. Notably, for young people, the stress level fluctuates, reaching peaks at months 12 and 24. In contrast, for older individuals, the stress level steadily decreases in the first year, remains stable in the second year, and then increases.
You may have noticed that the curve for young people resembles a piecewise linear function. Indeed, we can define this curve as a set of linear functions at specific intervals, as follows:
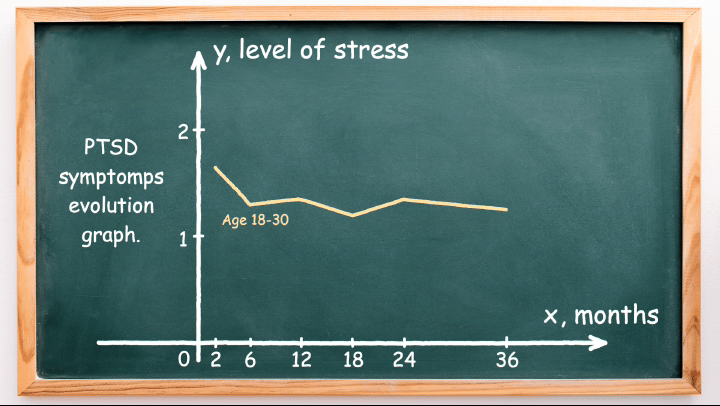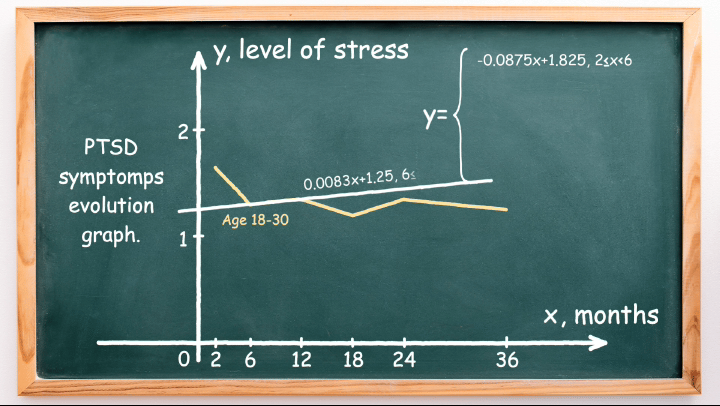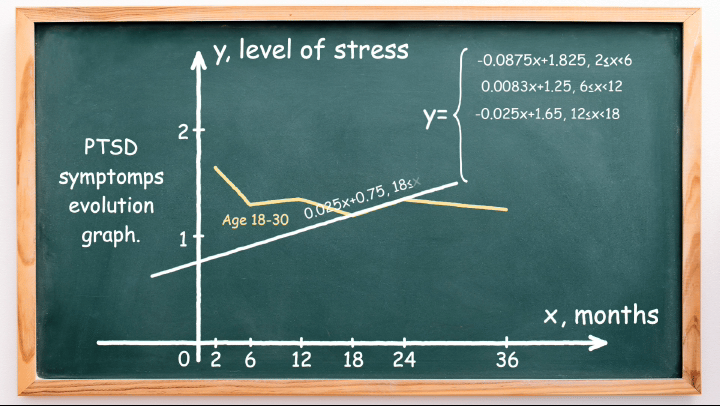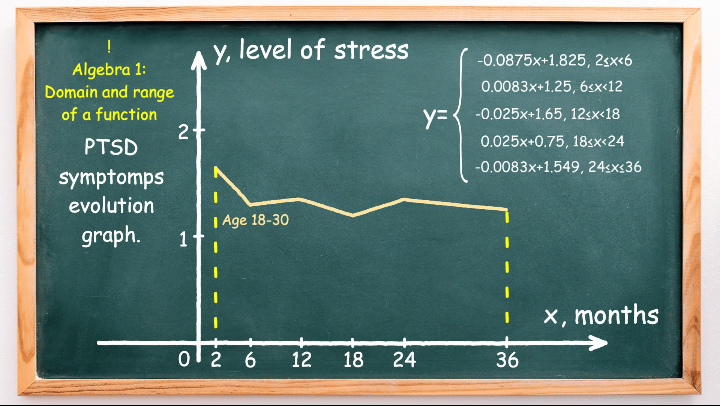
- The first piece is \(-0.0875x + 1.825\), in the interval \(2 \leq x < 6\).
- The second piece is \(0.0083x + 1.25\), in the interval \(6 \leq x < 12\).
- The third one is \(-0.025x + 1.65\), in the interval \(12 \leq x < 18\).
- The fourth function is \(0.025x + 0.75\), in the interval \(18 \leq x < 24\).
- The fifth is \(-0.0083x + 1.549\), in the interval \(24 \leq x \leq 36\).
These five functions form the piecewise linear function in the domain from 2 to 36, as illustrated in the animation below:
What Happens After Finding a Set of Linear Functions?
Once we’ve identified a set of linear functions that fits our data, specialized computer software can automatically analyze this information and generate forecasts. For instance, the software can predict the potential number of people requiring assistance from psychologists in the next 12 months. It can then automatically check if the district has a sufficient number of psychologists available. If there’s a shortage, local governments can take necessary measures.
Conclusion:
This example illustrates how public health specialists predict the number of individuals who may require medical assistance in the future. It showcases the impressive predictive power of mathematics. Once we can describe a phenomenon in mathematical language, we gain the ability to make accurate forecasts. In this instance, we’ve used mathematical language to describe how the stress levels of people change over time.
References:
During the preparation of this article, we relied on the following scientific publication:
In addition, the following video, issued by the National Collaborating Centre for Infectious Diseases (Canada), explains the basics of mathematical modeling in public health:
Video version
Further reading:
In the beginning of this article, we have shown two graphs – one modeling the development of PTSD symptoms for young people (our current example) and another modeling symptoms for older people. The curve for older people can also be modeled using mathematical functions (particularly quadratic functions), and we have a blog post explaining that. So, if you are familiar with quadratic functions, the following article is for you:
This article serves as an excellent example of the interconnectedness between math and psychology. Additionally, explore another article that delves into a different example showcasing the connection between math and psychology:
Finally, understanding this article requires an understanding of what a Cartesian coordinate plane is. If you are interested in how Cartesian coordinates are used in other real-life scenarios, then the following blog post is for you:
