Calculating Car Overtake with Systems of Linear Equations
Introduction
Ensuring the utmost safety is a top priority for every self-driving car. To achieve road safety, the car must predict and avoid potential dangers. Surprisingly, the systems of linear equations taught in high school play a crucial role in making these predictions. Let’s explore a specific example.
Linear Equations Describing Motion
Consider these two cars: the red car is moving at 40 mph, while the white car, a self-driving vehicle, is traveling at 60 mph with the intention of safely overtaking the red car before the ‘Do not pass’ sign:

To ensure a secure overtake, let’s create a mathematical model using linear equations.
The red car’s speed of 40 mph converts to approximately 58.67 feet per second (fps). Thus, the linear equation describing how the distance (y) depends on time (t) for the red car is:
\[y = 58.67t\]
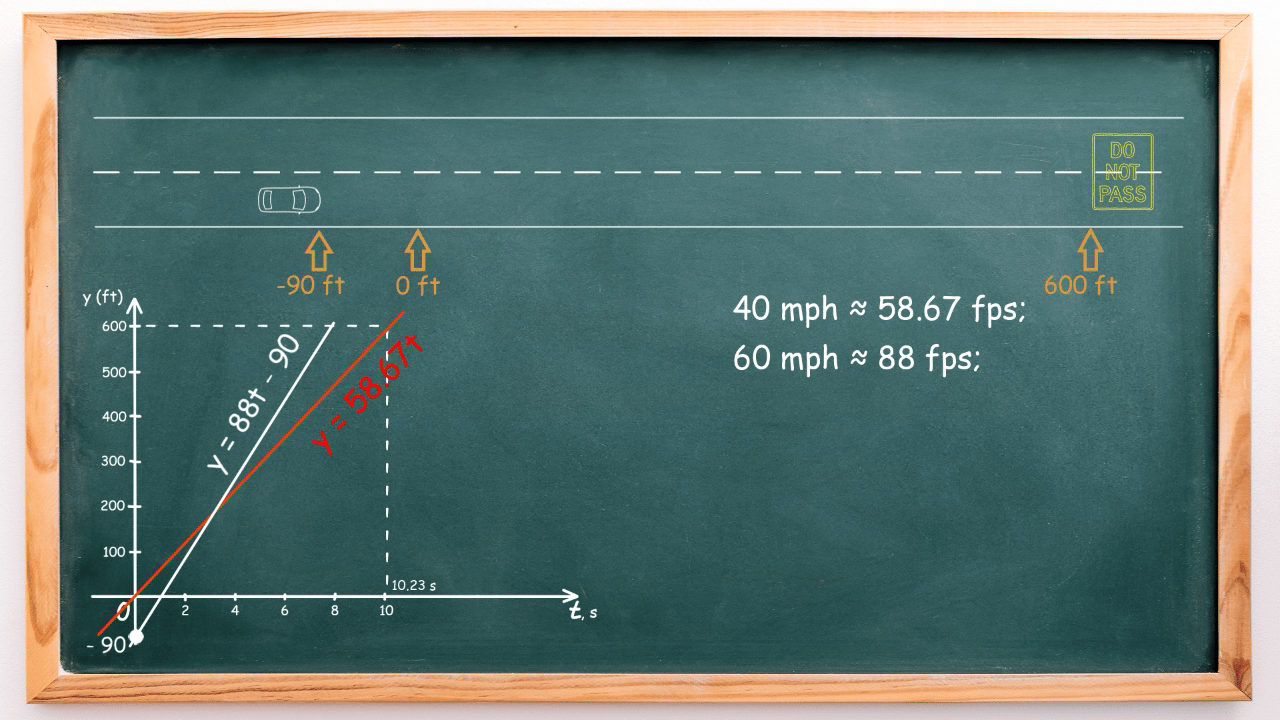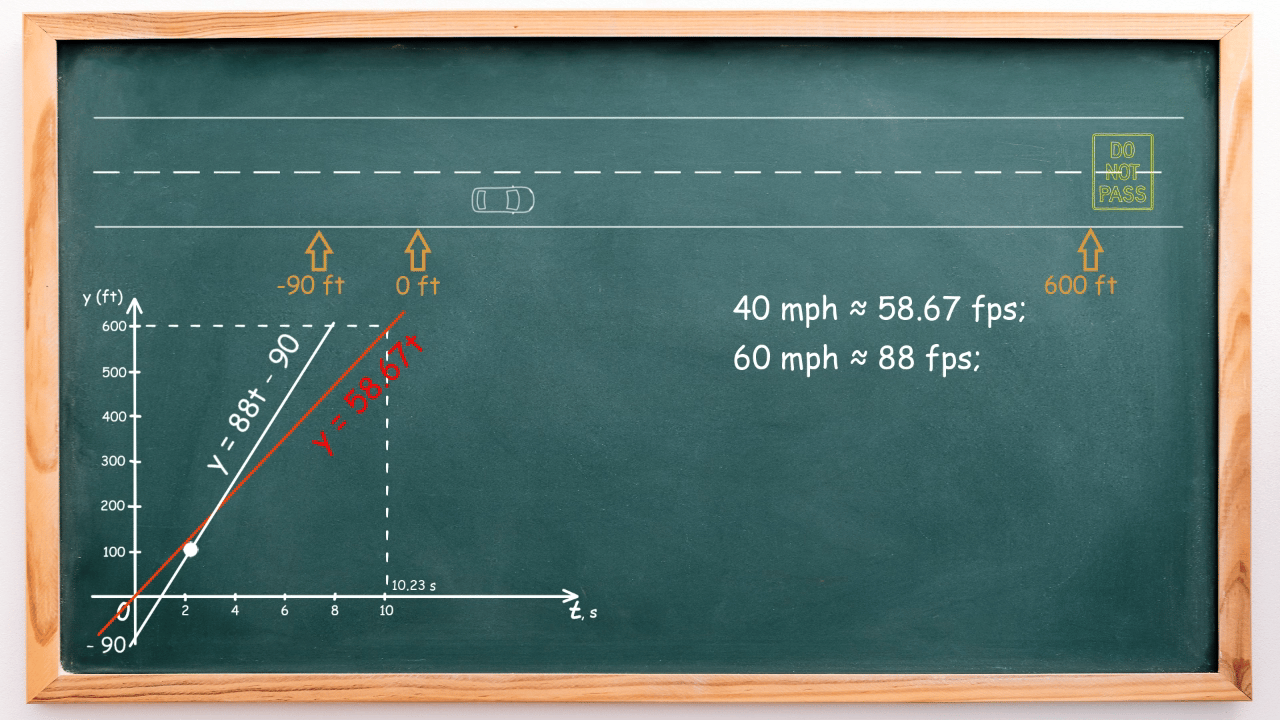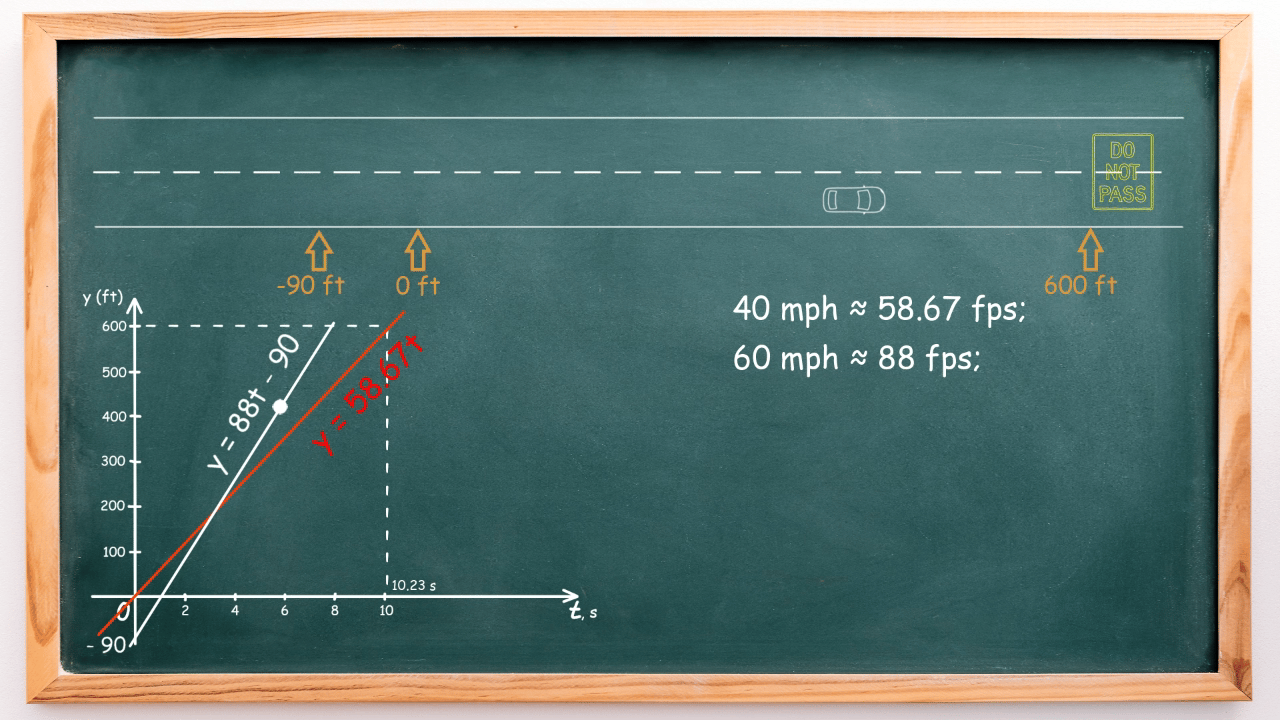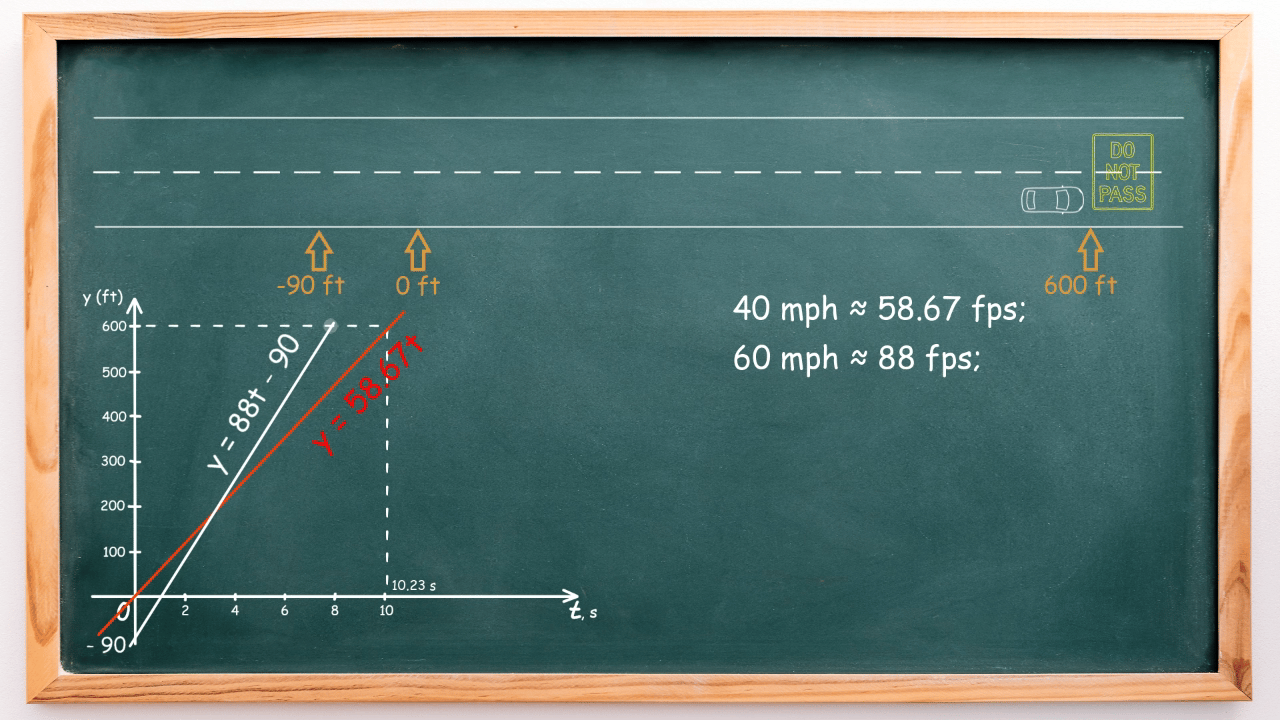
On the screen, observe how the car’s movement aligns with its mathematical model.
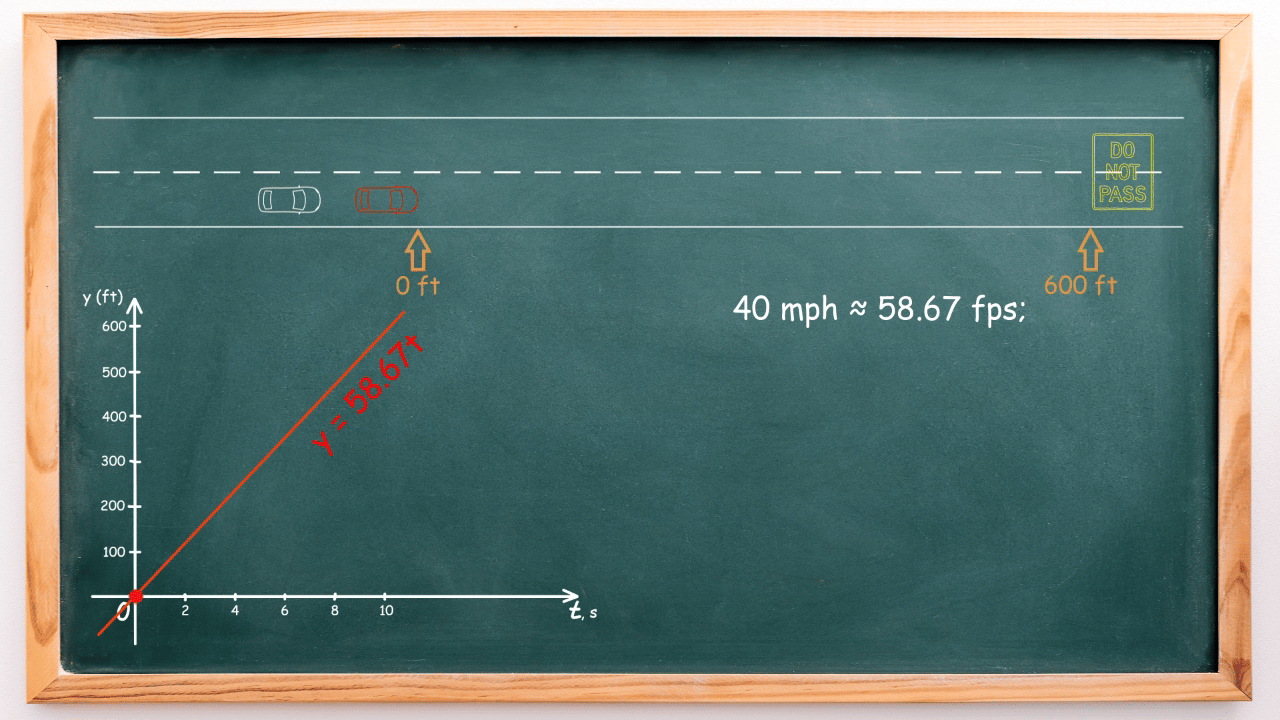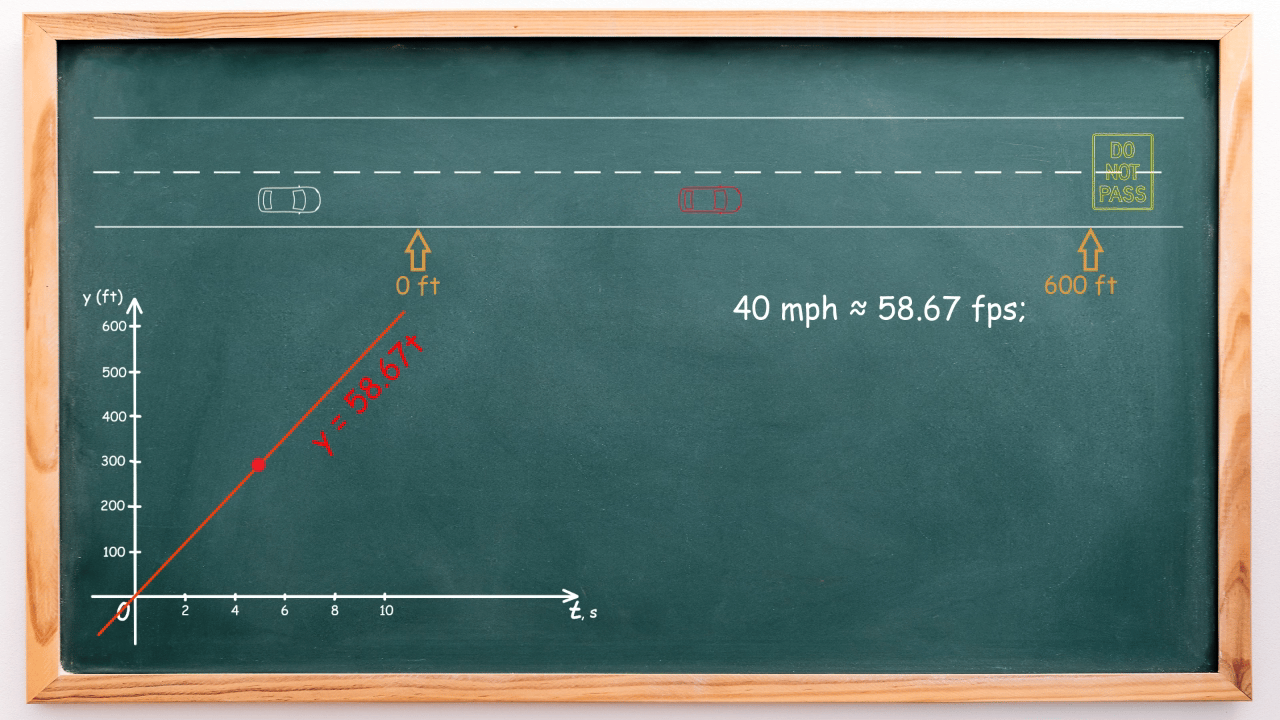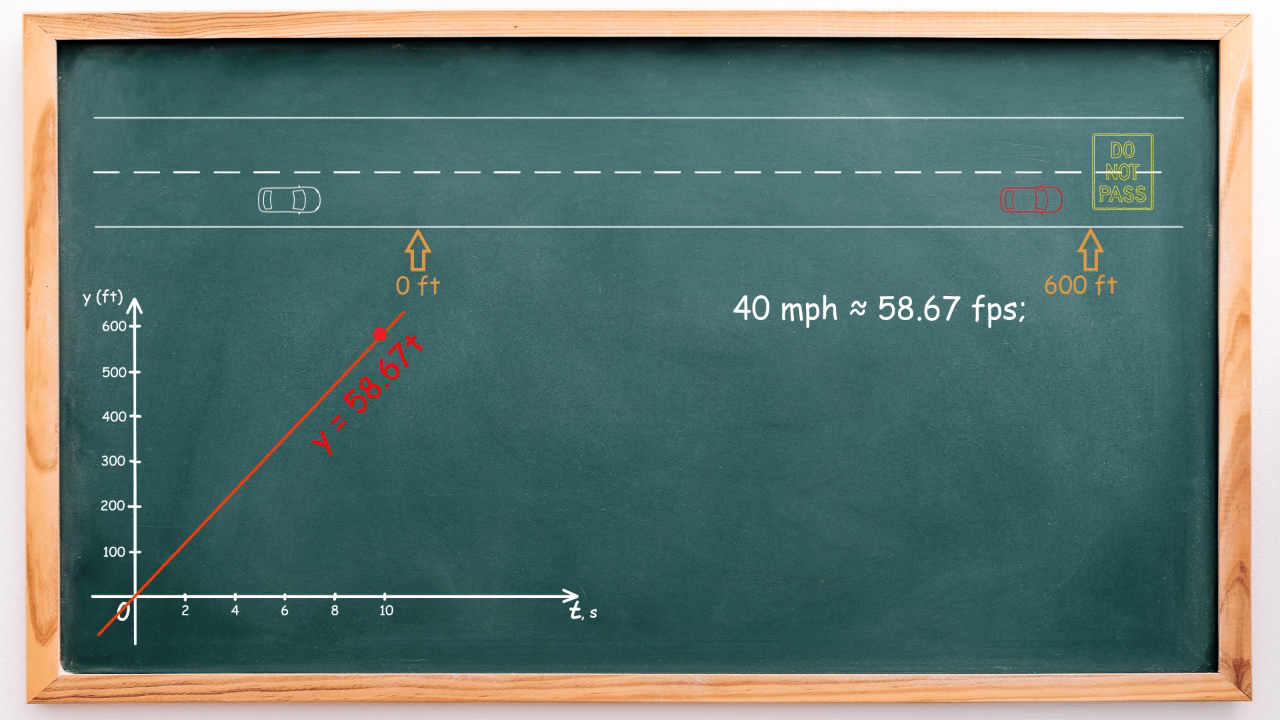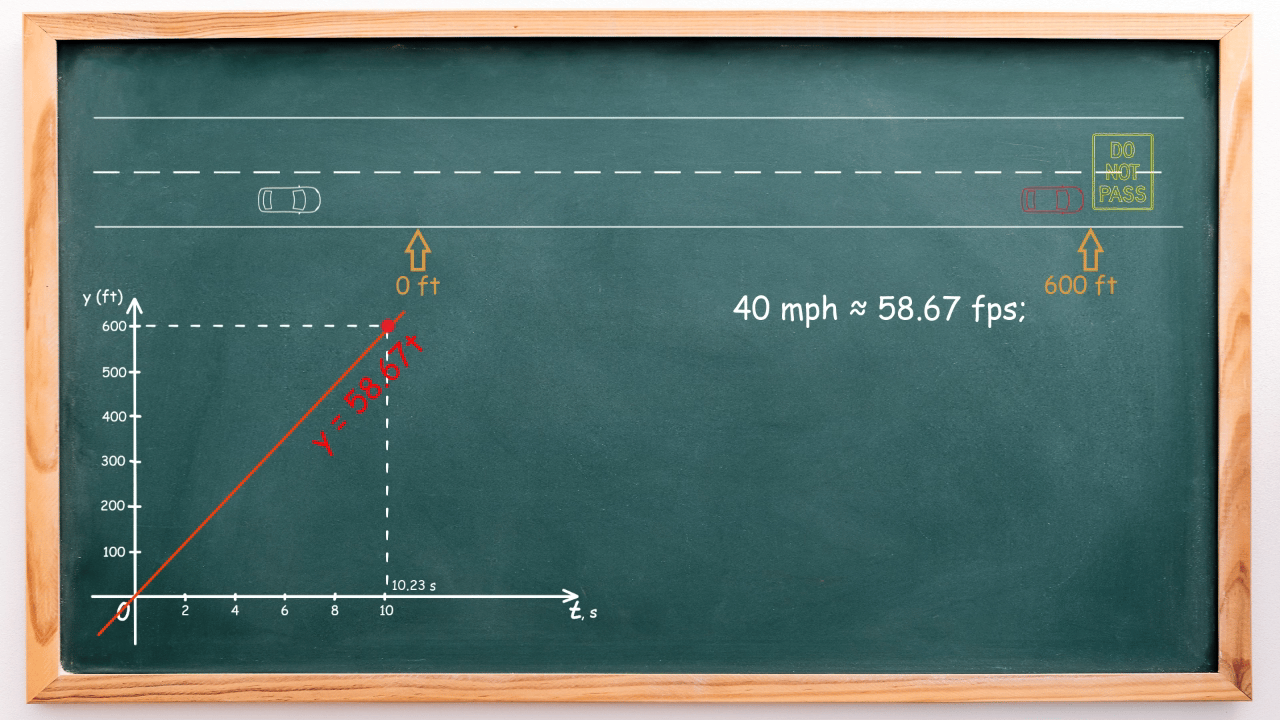
Meanwhile, the autonomous car is moving at 60 mph, approximately 88 feet per second (fps), and is positioned 90 feet behind the red car. Its linear equation for movement is:
\[y = 88t – 90\]
Let’s observe how the car’s motion corresponds to its mathematical model on the screen:
Solving System of Linear Equations
If we plot these two graphs on the same coordinate plane, we observe their intersection, representing the time moment when both cars are in the same place:

To determine this time, we solve the system of linear equations:
\[
\begin{cases}
y = 58.67t \\
y = 88t – 90
\end{cases}
\]
Using the substitution method, set the two expressions for \(y\) equal:
\[ 58.67t = 88t – 90 \]
Solving for \(t\):
\[ 29.33t = 90 \]
\[ t = \frac{90}{29.33} \approx 3.07 \]
Substitute \(t\) back into the first equation to find \(y\):
\[ y = 58.67 \times 3.07 \approx 180.02 \]
The solution is \(t \approx 3.07\) and \(y \approx 180.02\). Therefore, the calculated time is around 3.1 seconds, with a traveled distance of about 180 feet. This means the cars will be at the same position approximately 3.1 seconds after starting, at a distance of 180 feet.
What it Means for the Safety of the Overtake?
We’ve determined the time when the two cars are side by side. Similarly, we can calculate the time it takes for the self-driving car to return to its lane and determine if it can do so before the ‘Do not pass’ sign. This calculation is the fundamental principle behind how a car computer assesses whether an overtake is safe or not.
Conclusion:
You’ve just witnessed how intelligent systems, such as autonomous cars, are trained to evaluate safety and make decisions. While this example is somewhat simplified, real self-driving cars consider additional variables like road conditions, wind direction, and more. Nevertheless, the fundamental principle of solving systems of equations remains consistent, as demonstrated above.
Hands-On Exercise:

References:
We consulted the following scientific publications to prepare this article:
- Diachuk, M., Easa, S. M., Hassein, U., & Shihundu, D. (2019). Modeling passing maneuver based on vehicle characteristics for in-vehicle collision warning systems on two-lane highways. Transportation Research Record, 2673(9), 165-178.
- Scheel, Oliver, et al. ‘Attention-based lane change prediction.’ 2019 International Conference on Robotics and Automation (ICRA). IEEE, 2019.
Video Version:
We’ve also created a video version of this article. In the video, all car motions are presented in an animated format, making it easy to follow and understand the relationship between linear equations and motion on the road. Additionally, the video delves deeper by illustrating an example of solving a system of linear equations, which includes the position of the ‘Do not pass’ sign, to calculate the time when a self-driving car will reach this sign.
Enjoy the preview of the video below or subscribe to gain access to the full version.
Further Reading:
Self-driving cars are just one area where linear functions, in general, and systems of linear equations, in particular, play a crucial role. If you’re interested in exploring more about how linear relationships are applied in real life, feel free to dive into the following articles:
- Linear Function: A Real-Life Example (from Entertainment);
- Piecewise Linear Function: A Real-Life Example (Public Health).
Self-driving cars, as a topic, have a significant impact on various jobs. We also have an article that explains how the emergence of self-driving cars could influence the job of lawyers:
