Preview
Quick preview of what this blog post is about:
Linear function for controlling stage lamps
Introduction:
A linear function in the form of \(f(x) = mx + b\) is a first mathematical function you learn in school. You learn about slope and y-intercept, build its graph, and study how to recognize a linear function from tables. But did you know that a linear function is also a practical and handy tool that people use in lots of different areas, such as working with modern technological instruments or planning financial matters?
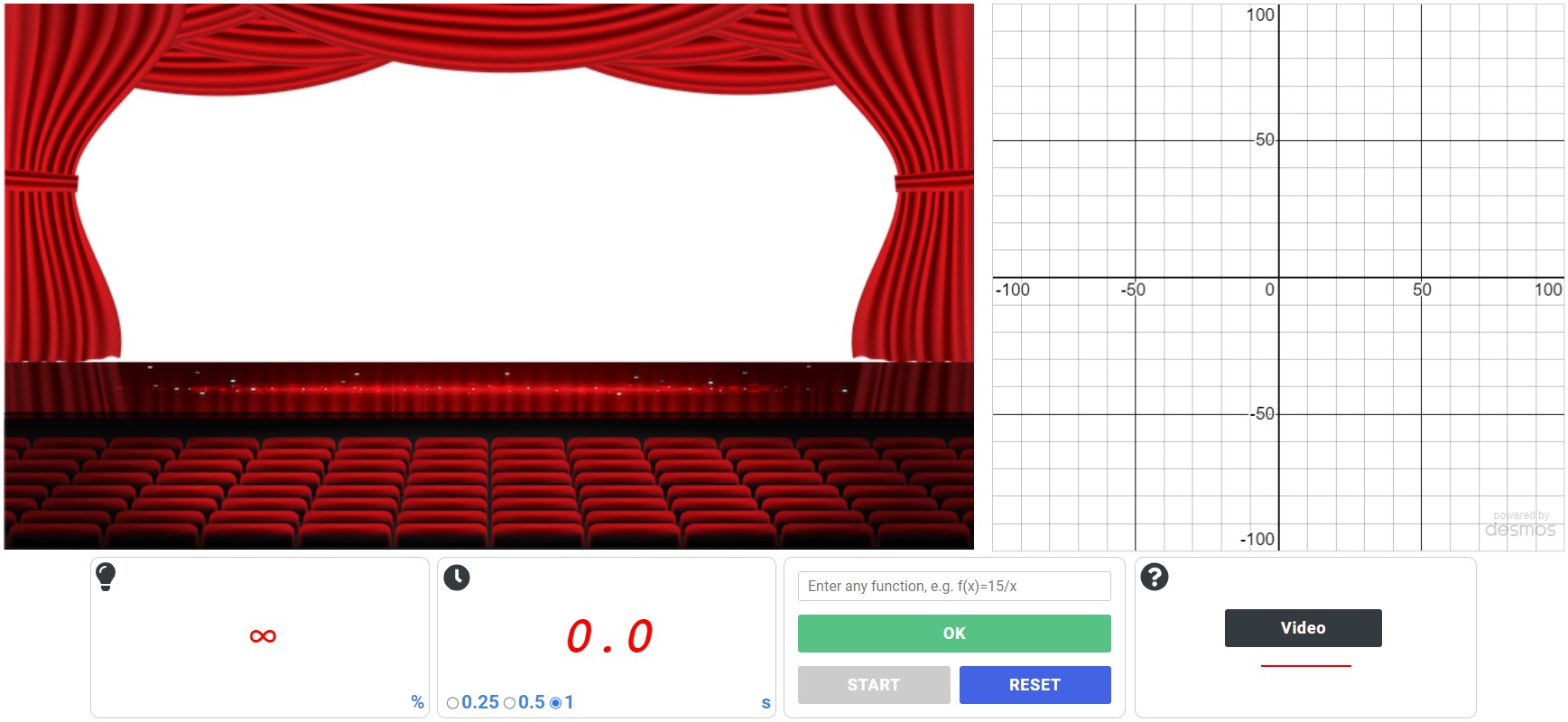
Take, for example, controlling the light during a theatre performance or a concert – like on the picture below. Did you know that linear functions are actually used for that?
Let’s have a more in-depth look: how can we control the light? Lighting specialists use special software and controllers for that, like the one in the picture below. The software in these controllers often knows how to control the light using linear functions.
Example:
Let’s take a specific case: fading the light in or out. Have a look at the Cartesian coordinate plane below. Let \(x\) (independent variable) correspond to time, and \(y\) (dependent variable) correspond to luminosity. This means that we can control the luminosity over time. Now, let’s consider the linear function \(y=2x\). The slope, equal to 2, indicates that we can increase the luminosity by 2% each second. In other words, in 1 second, the luminosity will be 2%; in 2 seconds — 4 percent, and so on. In 50 seconds, the lamp will shine at its full luminosity: \(y=2 \times 50=100\)%. This process is shown in the animation below.
Try it!
Exercise:
Suppose we have a function \(y = -\frac{5}{2}x + 50\). Can you calculate how many seconds the lamp will fade out if it is controlled by this function?
Solution:
The y-intercept of this function indicates that the lamp will start fading away from 50%. The minus sign tells us that the slope of this function is negative. A slope of 5 over 2 means that every 2 seconds, the luminosity is decreased by 5%.
Fading out means that the luminosity becomes zero – i.e. we need to find the x-intercept of this linear function. Therefore, to find the time at which the luminosity becomes zero, we need to solve the following linear equation:
\(-\frac{5}{2}x + 50 = 0\).
Solving this equation gives us \(x = 20\) seconds for the lamp to fade away.
Interactive simulation:
Control stage lighting using any linear function and see the light behavior on the screen. Click the image above to open the simulation in a new window. Check the facts!
A lot of lighting controllers and software work with linear functions. You can make sure yourself. Try a Google search with the phrase ‘linear light dimming curve,’ and you will see a lot of straight line graphs that you now understand thanks to your knowledge of linear functions.
Your key takeaway for today:
A linear function is very useful when there is a need to control some process depending on time, such as the luminosity of light.
Video version
Further reading
Other Uses of Linear Functions in Real Life
Curious about more real-life applications of linear functions? The following article will explore how piecewise linear functions are utilized in public health to make forecasts:
Related Math in Real Life
In this example, in addition to the linear function, there were also other important mathematical concepts: the Cartesian coordinate plane and independent and dependent variables. Those who are interested in how these concepts are used in real life are welcome to read our related articles:
- Coordinate Plane: A Real-Life Example (from Medicine);
- Dependent and independent variables: A real-life example (from fire protection).
If you are already familiar with other mathematical functions, such as the quadratic function, you’re welcome to read an article on how the latter is used in real life: