Arctan (Inverse Tangent) Example from Forensics
Does Forensic Science Need Math?
Perhaps it can come as a surprise, but mathematical methods are widely used in forensics. While it’s a common misconception that forensic scientists rely primarily on biology or chemistry, such as finding traces of poisons or analyzing DNA from a hair, the reality is that math also plays a crucial role in forensic jobs. One example that requires the calculation of arctan is crime scene reconstruction, as exemplified below.
Crime Scene Reconstruction
Criminalists, also known as forensic scientists, reconstruct crime scenes to understand how crimes were performed. For example, in the investigation of shooting scenes, they often need to determine the shooting angle and the suspected path of the bullet. Criminalists may use plastic strings or laser beams to determine bullet trajectories. However, this is not always possible, for example, if some objects like trees or bushes occlude the crime scene. This is where inverse trigonometric functions, particularly inverse tangent (arctan), come to the rescue.
How to Calculate Arctan: an Example
Consider a shooting scene where the bullet has entered and exited the wall, as shown in the animation below.
This scene can be modeled with the right triangle model (ABC), where:
- AB is the hypotenuse, formed by the flight of the bullet through the wall;
- Leg AC is a ‘horizontal’ leg (if the shooting scene is viewed from above);
- Leg BC is the ‘vertical’ leg.
- The angle α, formed between the path of the bullet and the wall, is the shooting angle we want to find.
The model, along with dimensions, is illustrated in the schematic below.
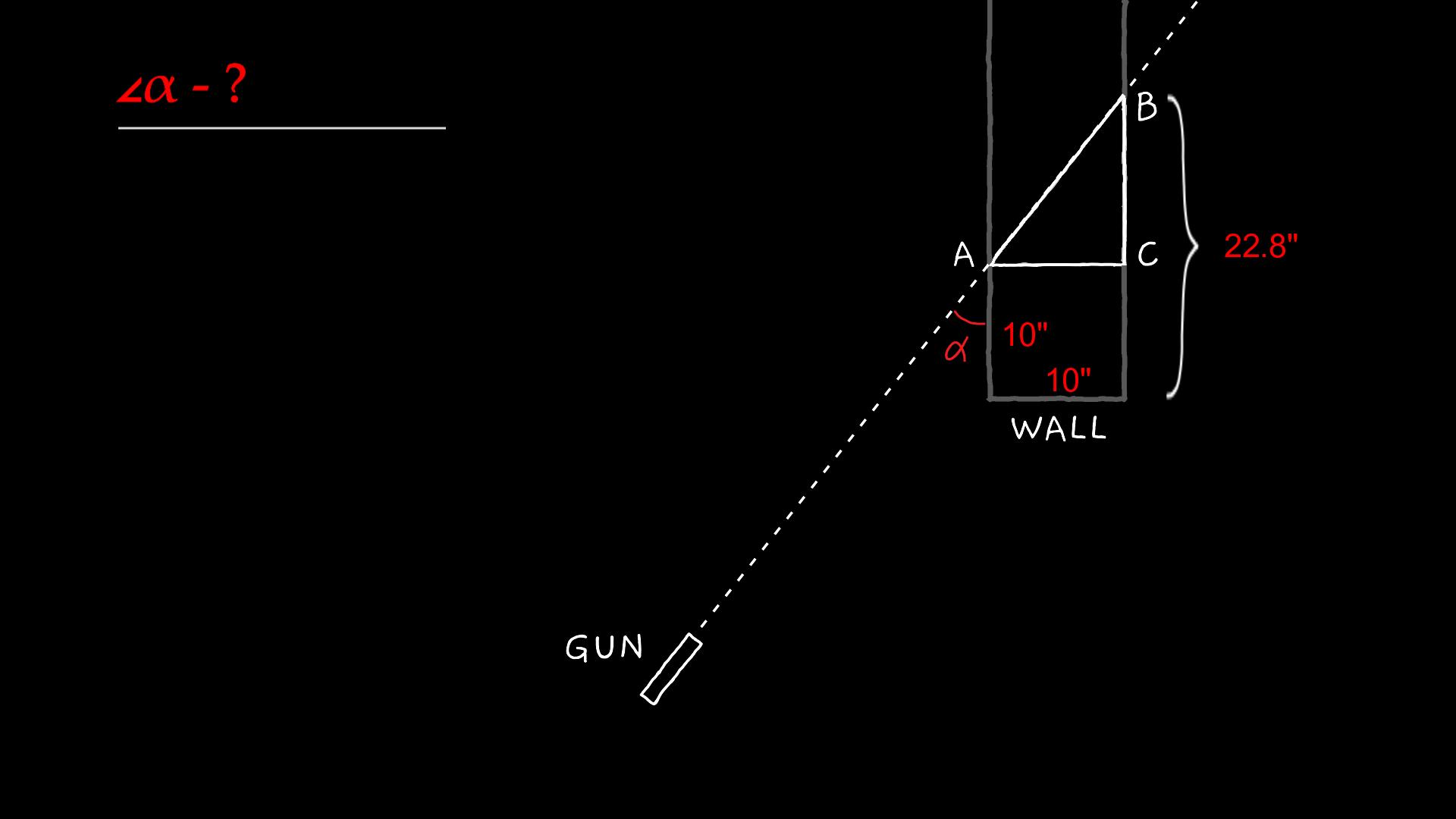
Angles α and ABC are corresponding angles, and therefore equal. To calculate angle ABC, you need to consider the lengths of the opposite leg (AC=10”) and adjacent leg (BC). AC is known, let’s find BC:
\[ BC = 22.8 – 10 = 12.8” \]
Then:
\[tan(\angle ABC) = \frac{AC}{BC}\]
and therefore:
\[tan(\angle ABC) = \frac{10}{12.8} = 0.78125\]
Finally, we have all the data to find arctan(0.78125):
\[ \arctan(0.78125) \approx 38° \]
Therefore, the angle ABC is approximately 38°, indicating that the shooting angle (α) is also approximately 38°.
Conclusion:
In this example, we created a model of a right triangle to reconstruct the shooting scene and then used arctan to find the shooting angle.
As you have just seen, high school mathematics is not an abstract science but has very specific applications used by ordinary people in their jobs – in our example, it was forensics. The same applies to science – a lot of knowledge gained in physics, chemistry, or biology classes is used, in one way or another, in different workplaces.
Check the Facts!
One of the publications we used to create this blog post is:
However, this example is not the only one demonstrating how inverse trigonometry is used in forensics. There are other applications as well, such as analyzing blood stains. Conduct a Google search with keywords like “trigonometry in forensics” to see for yourself how mathematical methods are indeed very useful for crime investigation.
Video version
We also have a video version of this article where we explore the uses of science in forensics. It includes more examples and animations. Check out the preview below or subscribe to the full video.
Further reading:
In this example, besides learning about arctan and inverse trigonometry, understanding angle geometry was important (remember corresponding angles ABC and α from the previous example?). If you want to explore more about how angles are used in real-life situations, check out the following article: