Table of Contents
Adjacent Angles in Architecture
Introduction
You might already know that math, especially geometry, is crucial for architects and construction engineers. The knowledge of geometrical properties of angles helps them create the most efficient and optimal solutions for various buildings. Let’s have a look at one specific example.
Optimal Angle for Solar Panels on Roof
One of the emerging architectural and construction requirements today is the use of various renewable energy solutions integrated into the building. For example, consider this building equipped with solar panels:
As you can see, solar panels are integrated into the south-facing roof sections. But if we cover the north-facing area with highly-reflective, mirror-like material, then a significant amount of sunlight can be reflected into the solar panel to increase its efficiency – as shown in the animation below:
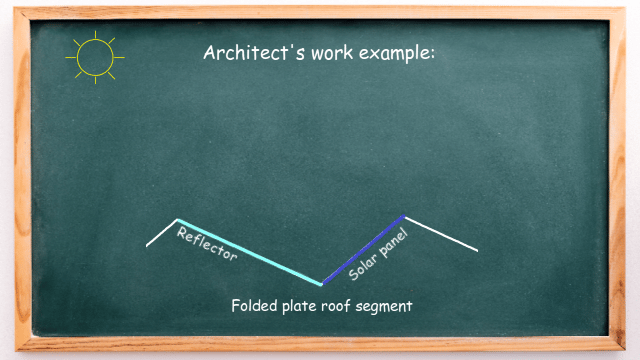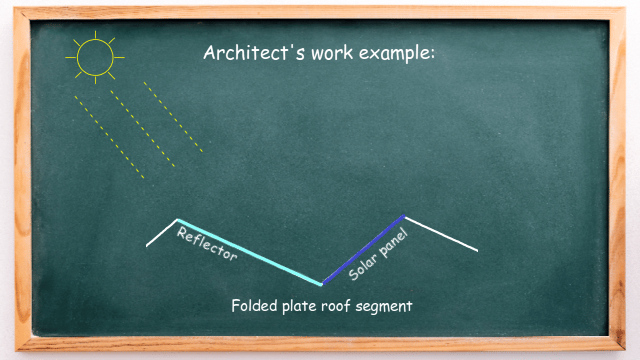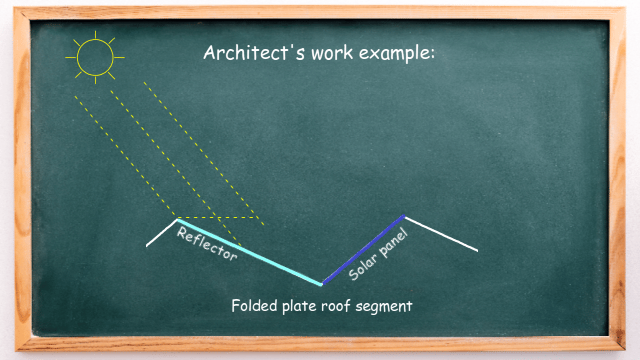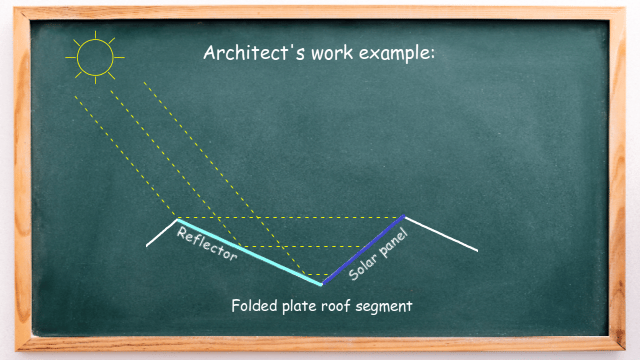
But the question an architect must deal with is: what should be the angle of the reflector so that the sunlight is directed straight to the solar panel? This is where adjacent angles and alternate angles are used to make calculations.
At DARTEF, we create engaging and easy-to-understand videos for students, showing how the math they learn in school is applied in real life. Here, you’ll find a preview of a video related to this article. If you enjoy it, consider starting a 7-day free trial to access more videos that explore the real-life applications of math.
Usage of Adjacent Angles and Alternate Angles: Step-by-Step Calculation
Let’s build a mathematical model of this system, as shown in the drawing below:
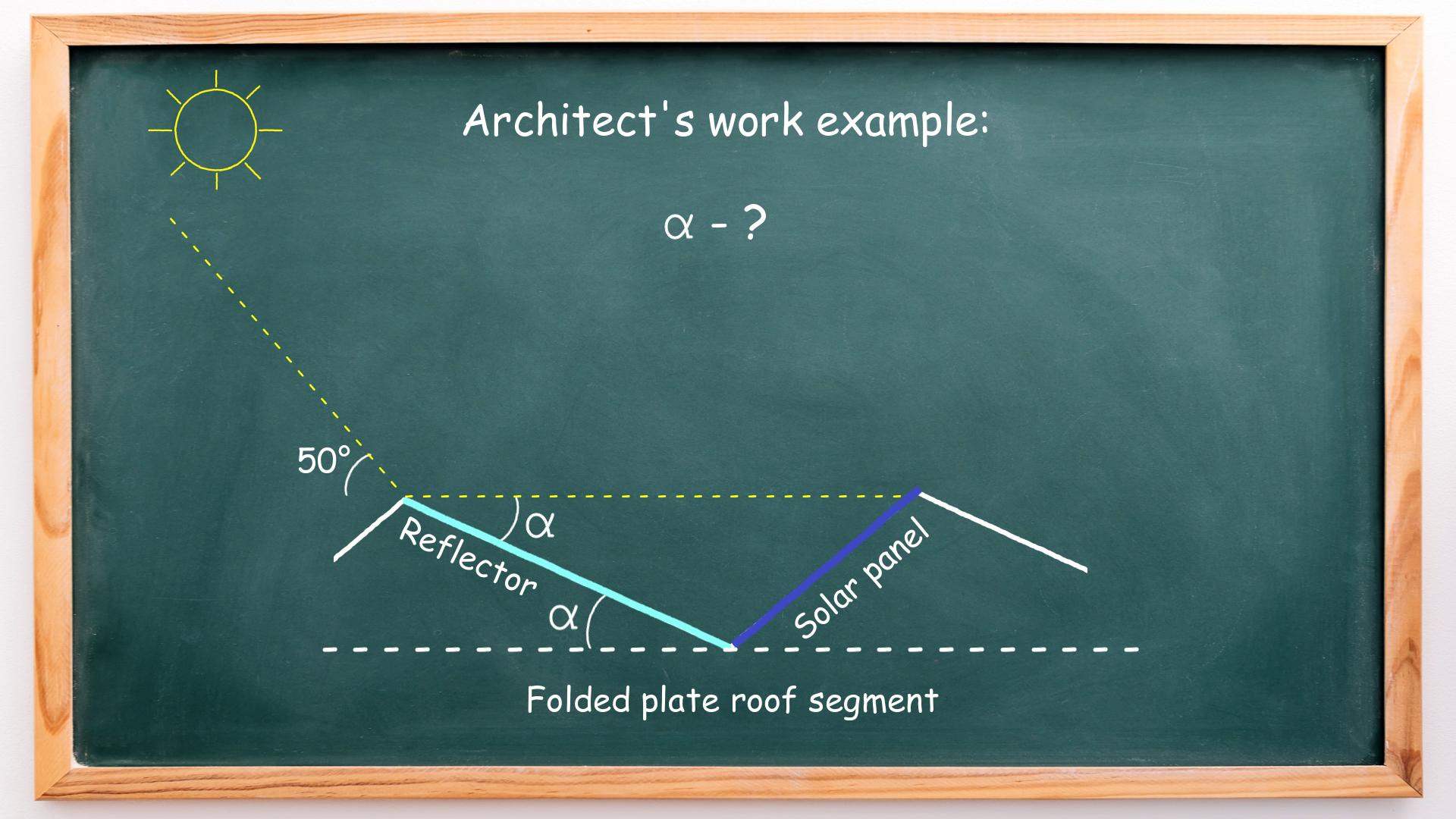
We need to reflect the sunlight with an incidence angle of 50° to the solar panel. The angle between the ray of reflected light and the reflector and angle α are alternate angles and, therefore, equal.
Next, the incidence angle (of 50°) and the angle β share a common side and common vertex and, therefore, are adjacent angles. It means that angle β equals 130° (180° – 50°). This is shown below:
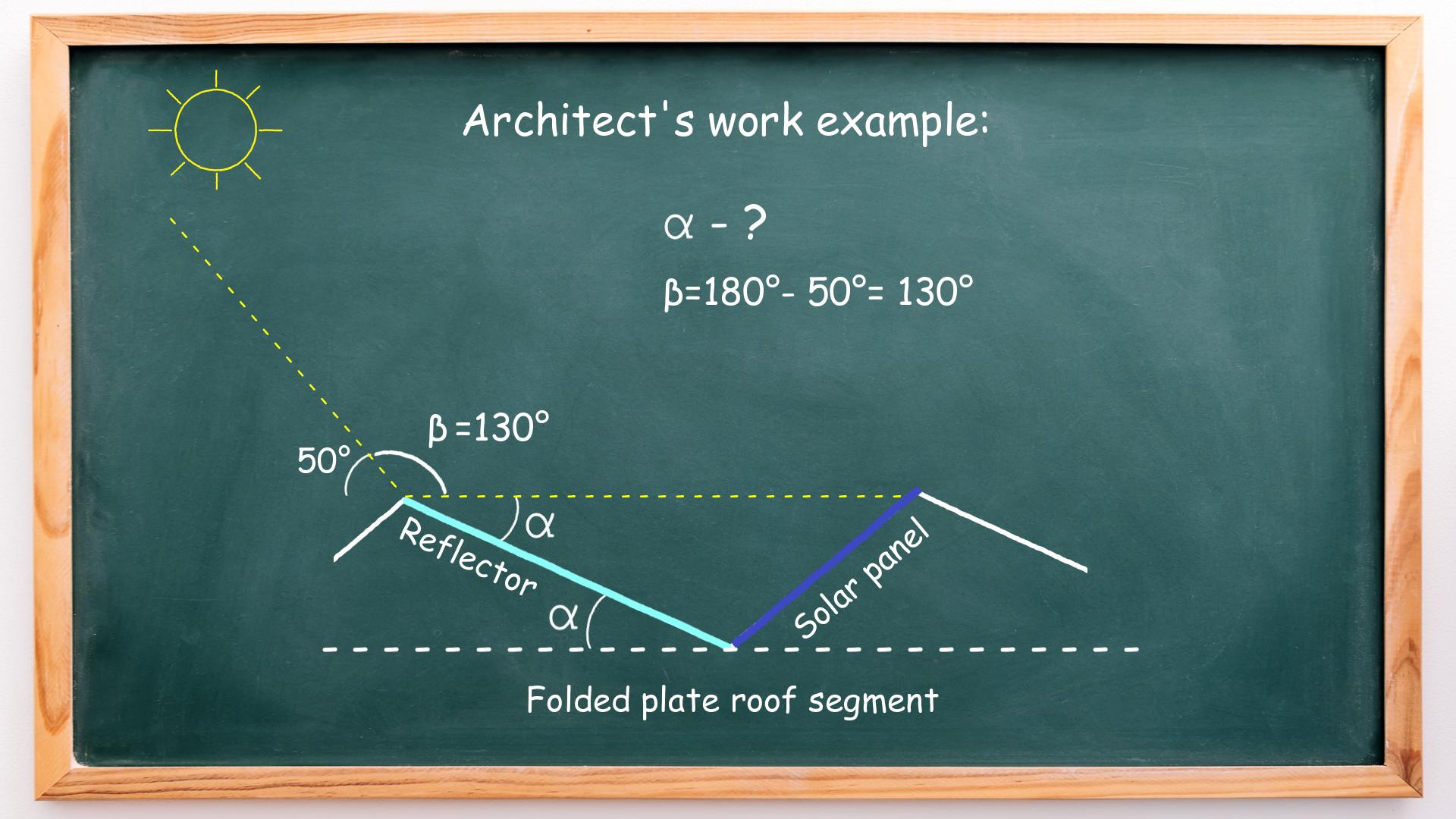
Next, let’s extend the line on which the reflector plane lies:
The newly formed angle also equals α and also shares a common vertex and common side with an angle β (thus, also forming adjacent angles). If angle β equals 130 degrees, then 2α equals 50°. Therefore, alpha equals 25°, and so does the reflector angle.
To answer our initial question, ‘What angle should the reflector be to direct sunlight straight to the solar panel?’ The answer is: an architect must use a 25° angle for the reflector when designing this roof.
Conclusion
This was an example of how the knowledge of adjacent angles and alternate angles helps architects and construction engineers make necessary calculations. As you have seen, this knowledge is very helpful when an architect needs to predict how the sunlight will travel. This is why mathematics is useful in life and jobs – it helps to predict how things will happen.
Video version
It is easier to follow the path of sunlight rays and the composition of adjacent angles in the animated video version of this article.
You can access this and other full videos by subscribing.
Check the facts
It’s no secret that mathematics and architecture are strongly connected. For those, who want to know more, here is one of the scientific publications that we used to create this article:
Further Reading
We have more real-world examples that can help you deepen your understanding of the geometry of angles! The following article will help you to understand how central angles are used in civil engineering for roadway design:
Additionally, if you are interested in other applications of math in architecture and construction, the following articles will be interesting to you: