Contents
Quick reminder of what parallel and perpendicular lines are
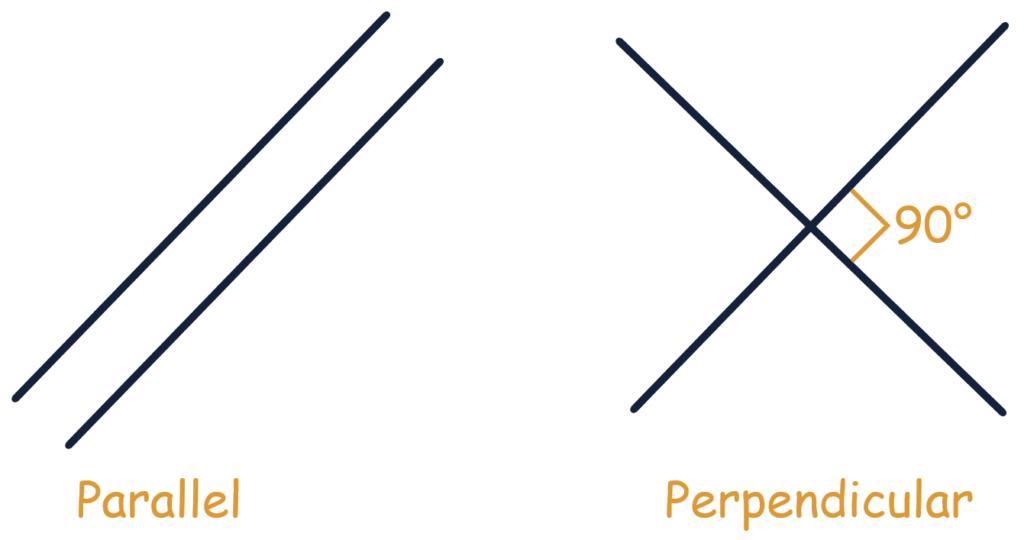
Parallel lines are two or more lines that never intersect, no matter how far they are extended. They maintain the same distance apart from each other at all points.
Perpendicular lines are two lines that intersect at a right angle, forming 90-degree angles where they meet.
Understanding these basic geometric concepts is essential for various fields in our daily and professional lives, from archaeology to engineering and beyond.
Parallel and perpendicular lines in real life – introduction
How does knowledge about parallel and perpendicular lines help people in their jobs? Parallel and perpendicular lines are widely used in several jobs. For example, in computer graphics, parallel and perpendicular lines are used to create geometric shapes, define boundaries, and determine perspective, necessary for creating realistic images and animations.
In civil engineering, parallel and perpendicular lines play an important role in designing roads, bridges, and buildings, helping engineers establish precise alignments, angles, and layouts for structural elements.
In landscape design, parallel and perpendicular lines are utilized to plan garden beds, pathways, and outdoor structures, ensuring symmetrical layouts, proper spacing, and aesthetically pleasing arrangements within outdoor spaces.
In such fields as archaeology and forensics, parallel and perpendicular lines help predict how the face of a human being looked when alive based on the shape of the skull. Let’s explore this example in more detail in the next sections.
Case Study
Reconstruction of Faces Using Geometry of Parallel and Perpendicular Lines
Julius Caesar, Cleopatra, Joan of Arc, and even Jesus Christ… Over centuries, people have been curious about the true appearances of famous historical figures. Beyond mere curiosity, there’s often a genuine need to understand how these individuals looked — for instance, in forensic investigations such as murder cases. This process is known as facial reconstruction. Both archaeology and forensics employ the same methods of biological anthropology to achieve this. Let’s explore how they utilize the geometrical properties of parallel and perpendicular lines through a real-life case study.
Nose Shape Reconstruction – An Example
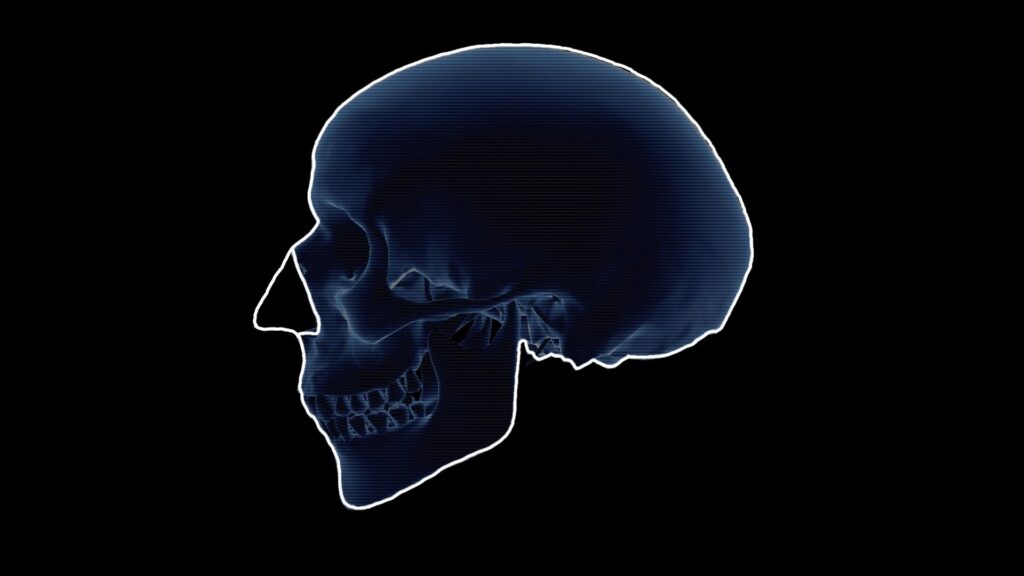
In this example, we’ll observe how drawing parallel and perpendicular lines aids in the reconstruction of the nose shape. Take a look at the model of a human skull in the picture below.
How can we determine the shape of the nose from this skull? One method involves utilizing the symmetry of the rim of the piriform aperture (Latin: Apertura piriformis) – a pear-shaped opening in the skull.
To accomplish this, the following steps are performed:
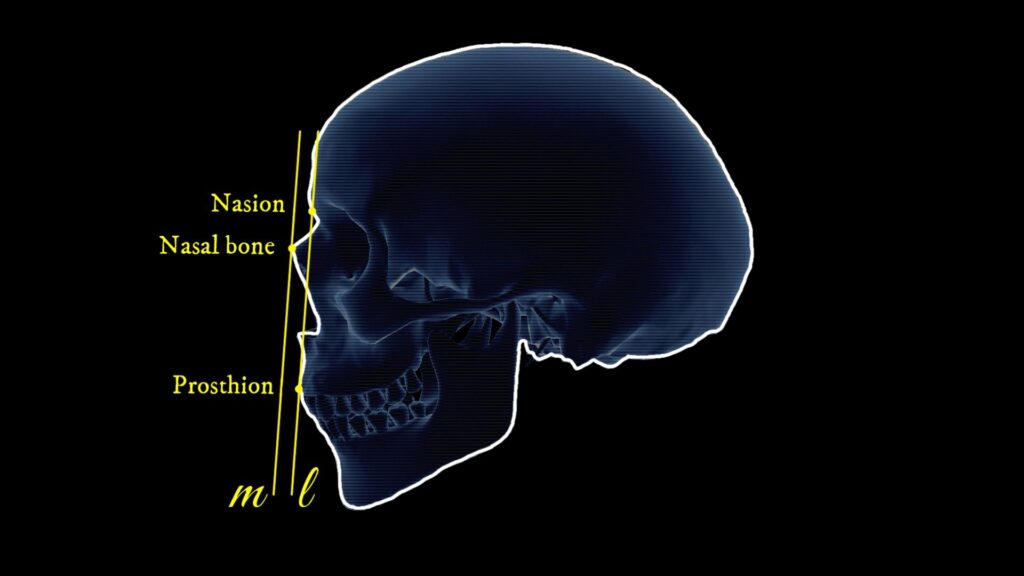
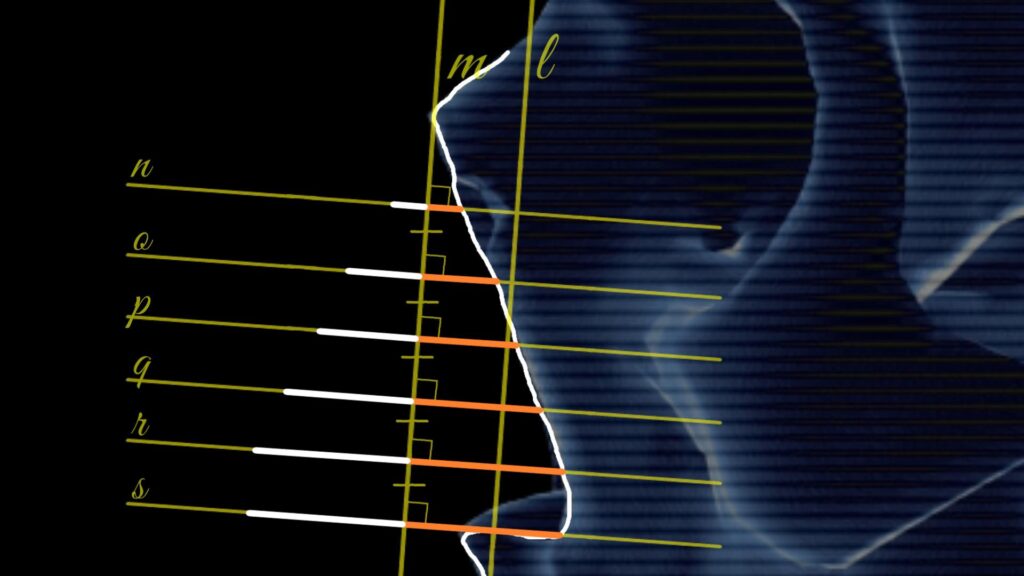
- First, a tangent line \( l \) is drawn with respect to two specific points of the skull: the nasion and prosthion. The line must be tangent to the prosthion and pass through the nasion, as illustrated in the figure below:
2. Next, a line parallel to line \( l \) is drawn. This parallel line, labeled \( m \), should pass through the foremost point on the nasal bone, as shown in the figure below:
3. Following that, six parallel lines are drawn, with each line perpendicular to line \( m \). It’s important to ensure that the distances between these lines are equal. These lines are labeled \( n \), \( o \), \( p \), \( q \), \( r \), and \( s \), as depicted in the figure below:
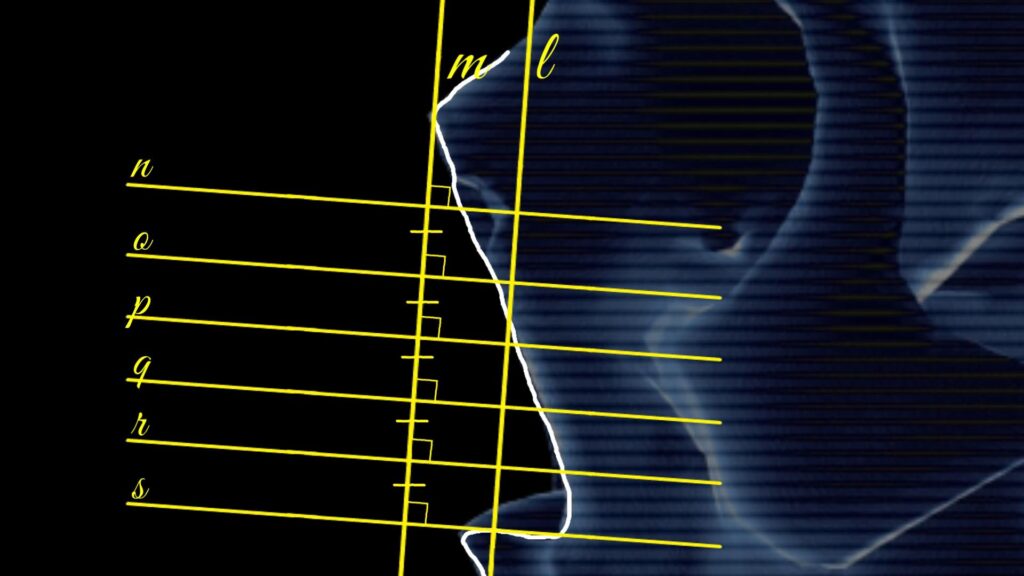
4. Now, let’s mark segments on each of these parallel lines. The right endpoint of each segment should align with the rim of the pear-shaped opening, while the left endpoint is plotted symmetrically to the right. For example, in segment AB, points A and B are symmetrical with respect to line \( m \).
5. As you can see, we now have a set of six points, each belonging to parallel lines \( n \), \( o \), \( p \), \( q \), \( r \), and \( s \). These points are: A, C, E, G, I, and K. By drawing a curved line through these points, we can approximate the likely shape of the nose of the individual whose skull we’re examining.
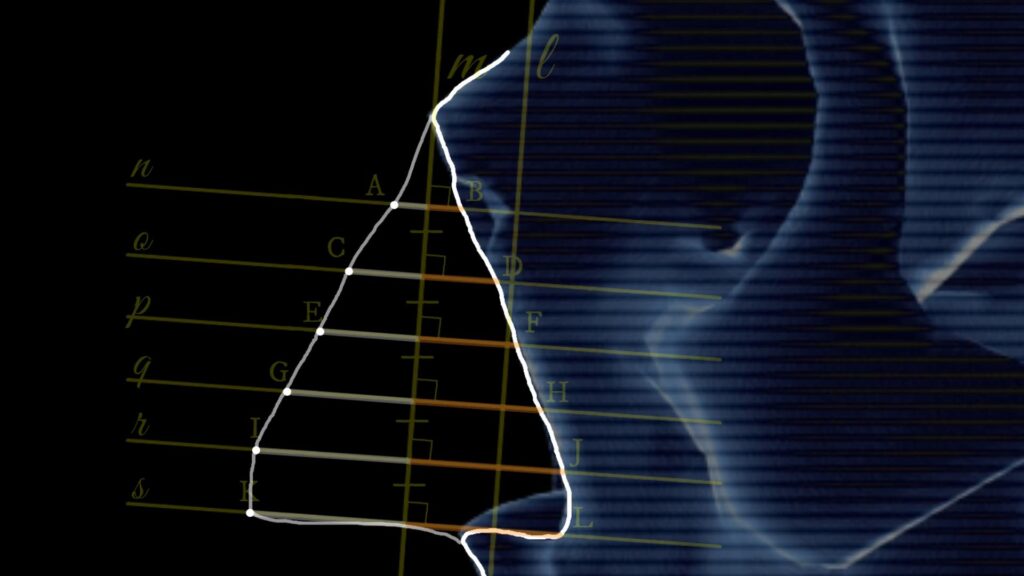
It’s important to note the term “likely” here. This method is based on statistical data collected over many years, providing the most probable match for the nose shape.
Conclusion
You’ve just witnessed how the geometry of parallel and perpendicular lines is applied in reality by biological anthropology specialists working in archaeology and forensics. As you can see, beyond knowledge of human anatomy, real-world constraints require us to understand many mathematical concepts learned in math lessons for this work. Concepts such as parallel lines, perpendicular lines, tangent lines, line segments, symmetry, and probability, as mentioned in this article, are crucial for these fields.
Classroom Version
If you want to share these examples with students in math class, we have a full version of the video available. This video explains the construction of parallel and perpendicular lines in just a few minutes and helps students connect what they learn in school with real-world applications. Additionally, it showcases real examples of reconstructed faces! Check the preview:
References
This method is described by both scientists and actual practitioners, such as the Federal Bureau of Investigation. We have consulted the following sources to prepare this article:
- Prokopec, M., & Ubelaker, D. H. (2002). Reconstructing the Shape of the Nose According to the Skull by Miroslav Prokopec (Forensic Science Communications, January 2002). Research and Technology, 4(1).
- Stephan, C. N., Henneberg, M., & Sampson, W. (2003). Predicting nose projection and pronasale position in facial approximation: a test of published methods and proposal of new guidelines. American Journal of Physical Anthropology: The Official Publication of the American Association of Physical Anthropologists, 122(3), 240-250.
Further Reading
In this article, we’ve explored a real-life application of the geometry of parallel and perpendicular lines in biological anthropology. We also have another article that, similar to this one, explains how math is used in biology:
Additionally, we offer more articles about how geometry is applied in various real-world scenarios!
- In the article “Alternate and Adjacent Angles: A Real-Life Example (from Architecture),” we explore how alternate and adjacent angles are used to make buildings more environmentally friendly.
- In the article “How to Find a Central Angle: A Real-Life Example (from Civil Engineering)” we explore how central angles are used in designing safe roadways.