Watch or Read?
Our video preview (right/below on mobile) shows how math and science shape real architecture:
Animated breakdowns of key concepts
Real construction examples using trigonometry
Career insights: Try on an architect’s problem-solving process.
Prefer text? Just keep reading!
Table of Contents
Short Summary
Tangent (trigonometry) is used in architectural and construction design to calculate the optimal length of roof overhangs depending on the solar angle. A roof overhang can be modeled as a right triangle where the adjacent leg is the length of the roof overhang, the opposite leg is the distance from the bottom of the window to the ceiling, and the hypotenuse represents the direction of the sunrays. Knowing the solar angle, it is possible to calculate the length of the overhang using the tangent function.
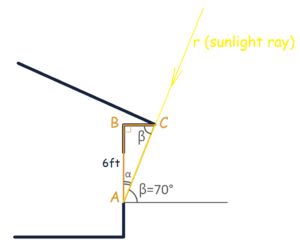
Keep reading for more information!
Quick Reminder About What Tangent Is in Trigonometry
The tangent function is a fundamental concept in trigonometry. In a right triangle, the tangent of an angle is the ratio of the length of the side that is opposite the angle to the length of the side that is adjacent to the angle. For example, in triangle ABC (see below), the tangent of angle α is the ratio of the length of side CB (opposite to the angle α) to the length of side AC (adjacent to the angle α).
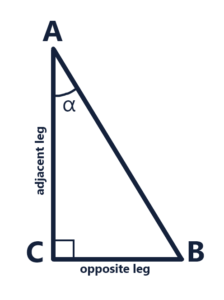
Mathematically, it is expressed as:
\[ \text{tan}(α) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{\text{CB}}{\text{AC}} \]
This function is particularly useful in real-life scenarios involving angles, distances, lengths, and more.
Tangent in Real Life
Tangent in Agriculture
In agriculture, the tangent function is used to align rows of crops. By calculating the angles of the fields and the positions of the rows, farmers can ensure optimal sunlight exposure and irrigation efficiency.
Tangent in Astronomy
Astronomers use the tangent function to calculate the angle of elevation when observing celestial bodies. This helps in determining the exact position and movement of stars and planets.
Tangent in the Energy Domain
In the energy sector, the tangent function helps determine the optimal angles for solar collectors and panels. This ensures maximum sunlight absorption and energy efficiency.
Tangent in Medicine
In medical imaging, the tangent function is used to interpret angles and distances within the body, aiding in accurate diagnosis and treatment planning.
Tangents are also very useful in architecture and construction for calculating the height of a building or determining the optimal size of a roof overhang. Let’s explore the latter in detail as a case study.
Case Study: Finding the Perfect Roof Overhang Using Tangent
Introduction: Why Roof Overhangs Matter

Roof overhangs are important architectural features that provide several benefits:
- Sun Protection: They offer shade, reducing the amount of direct sunlight entering windows, which helps in cooling the building and reducing energy costs.
- Rain Protection: Overhangs help protect walls and windows from rain, reducing the risk of water damage.
- Aesthetic Appeal: Overhangs contribute to the architectural style and visual appeal of a building.
To maximize these benefits, it’s crucial to calculate the optimal size of the overhang based on the sun’s position at different times of the year. In our example, we’ll see how the tangent function is used to calculate the length of the roof overhang for sun protection.
Using Tangent to Calculate Roof Overhang for Sun Protection (Florida example)
Let’s walk through a practical example to understand how the tangent function is used to calculate the optimal roof overhang.
Imagine a model of a house. Suppose we want to create an overhang that blocks the high summer sun (approximately from late April to early August) but allows lower winter sun to enter. We’ll use Florida as our example region.

Modeling the House and Its Roof Overhang via Right Triangle
Many architectural and construction elements can be modeled with the help of geometry, particularly right triangles. One such right triangle can be seen in the picture below:
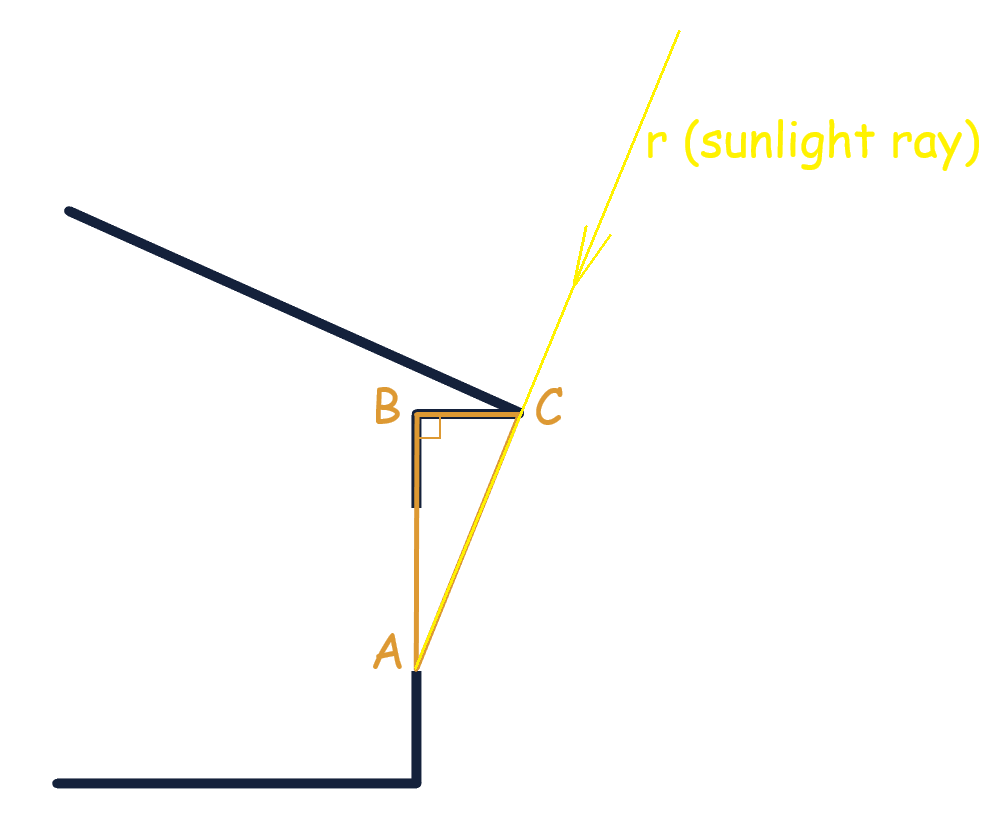
In the triangle ABC, leg AB is the distance from the bottom of the window to the roof overhang. In our example, this length is 6 feet. Leg BC is the length of the overhang that we need to determine, and AC is the hypotenuse that lies on the ray “r” representing the direction of the sunrays.
Calculating the Length of the Overhang Using Tangent (1st Method)
In Florida, from about late April to early August, the Sun reaches a 70-degree solar angle. Therefore, the solar angle β in our figure equals 70°. Angles β and α are adjacent, and therefore angle α equals:
\( 90^\circ – 70^\circ = 20^\circ \)
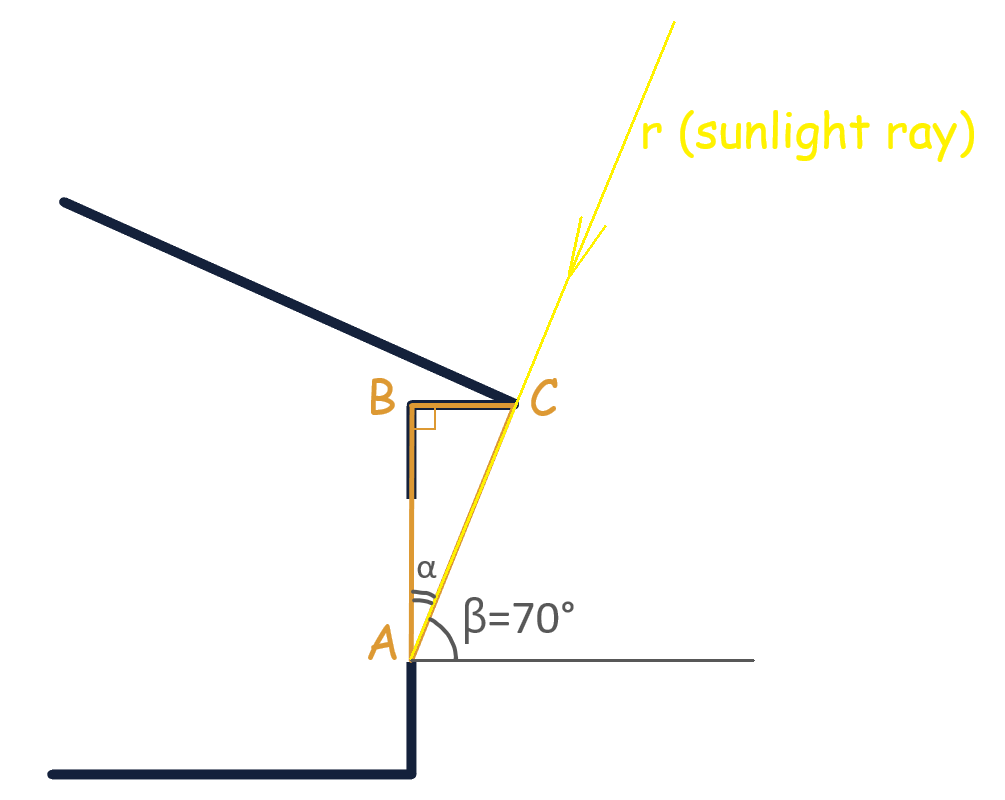
In our triangle, the leg BC is opposite to angle α, and the leg AB is adjacent to angle α.
Tangent α is:
\( \tan(\alpha) = \frac{BC}{AB} \)
Since BC is the length of the overhang that we need to determine, rearranging the formula to solve for BC gives us:
\( BC = AB \cdot \tan(\alpha) = 6 \, \text{ft} \cdot \tan(20^\circ) = 6 \cdot 0.36 \approx 2.2 \, \text{ft}. \)
Calculating the Length of the Overhang Using Tangent (2nd Method)
There is another way to determine the angle of the right triangle and calculate the length of the overhang using properties of alternate angles.
More precisely, angles β and ∠BCA are alternate angles and therefore equal. Thus, the angle ∠BCA = 70°.
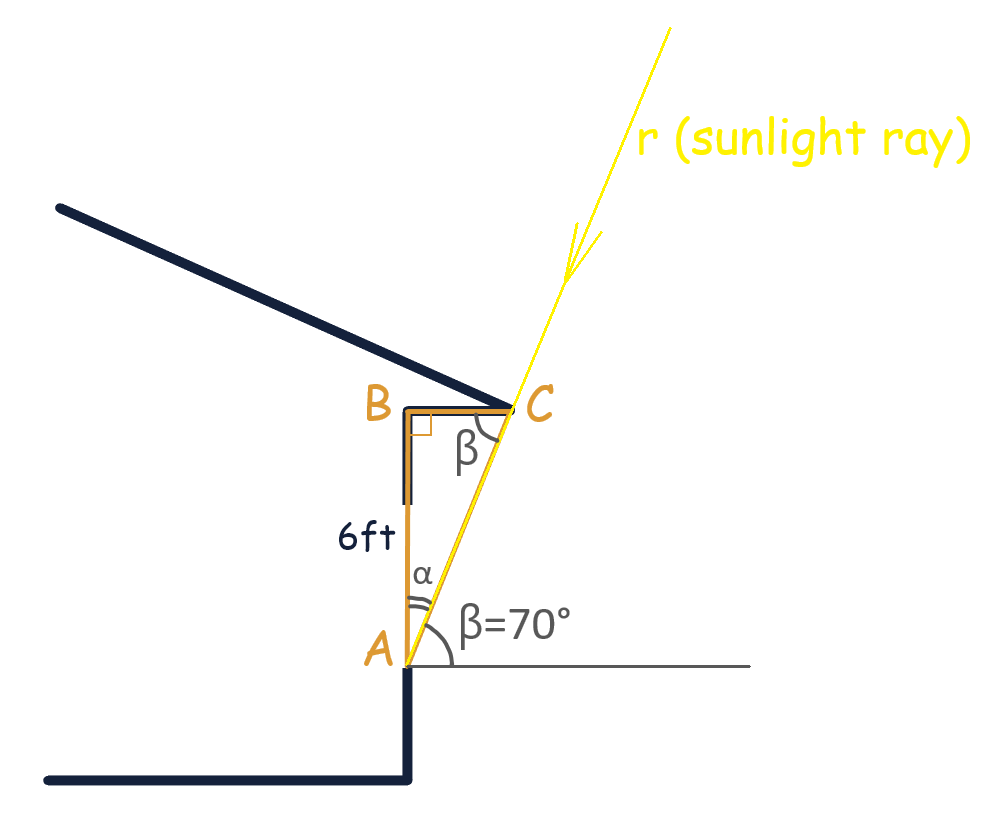
In the case of ∠BCA, leg AB is opposite and leg BC is adjacent to this angle:
\( \tan(\mathrm{BCA}) = \frac{AB}{BC} \)
Therefore:
\( BC = \frac{AB}{\tan(\mathrm{BCA})} = \frac{6}{2.75} \approx 2.18 \, \text{ft}. \)
Thus, in our example, the optimal roof overhang length should be approximately 2.2 ft to effectively block the high summer sun.
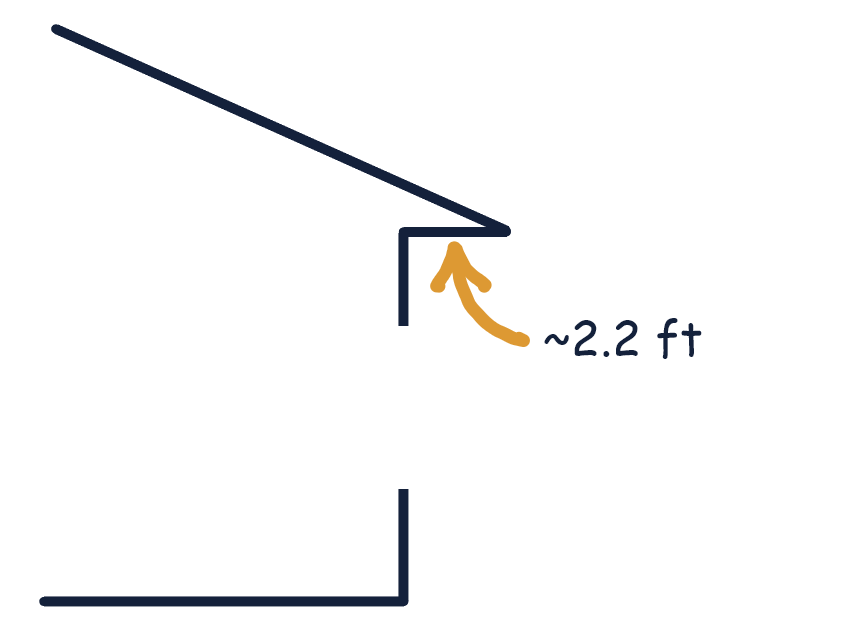
What if We Try This in a Northern State? (Minnesota Overhang Case Study)
At higher latitudes, the math works the same way—but the ideal overhang size changes. Our full video breaks it down with animations and real-world examples.
Perfect for:
Career discovery: See how math and science translate to architecture/design
Practical learning: Watch trigonometry solve actual problems
Future planning: Start exploring if this career path fits you
Preview the video to test-drive a day in an architect’s shoes!
Conclusion
The tangent function is a powerful tool in architecture and construction, providing a simple yet effective way to calculate the size of building elements, including roof overhangs. By understanding and applying this mathematical concept, architects and construction engineers can design overhangs that protect from sun and rain, enhance energy efficiency, and add to the visual appeal of buildings. So next time you see a well-designed roof overhang, remember the role of trigonometry and the tangent function in making it possible.
Worksheet
Download the worksheet for this real-world case study.
References
To ensure the accuracy of the information in this article, we have used the following publication:
Further reading
In this article, we have explored how tangent is used in architecture and construction. If you are interested in learning more about applications of trigonometry in real life, these articles might interest you:
- Find the Missing Side: A Real-Life Example (from Robotics)
- Cosx: A Real-Life Example (from Petroleum Engineering)
- Arctan: A Real-Life Example (from Criminology)
Additionally, if you are interested in other applications of math in architecture and construction, the following articles will be interesting to you:
