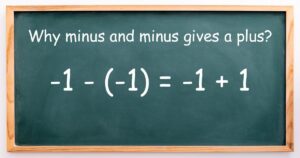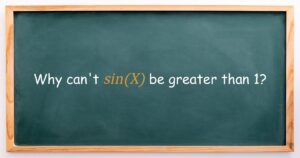Table of Contents
Who this article is for:
This article is designed for both parents and students who want to ensure a deeper understanding of math, beyond just memorizing procedures.
It addresses why students who performed well in elementary school often struggle with math in middle and high school and how to help them improve.
The article includes common mistakes that often lead to misunderstandings, which contribute to struggles in learning. These mistakes are grouped by grade level, and it’s emphasized that checking understanding of previous topics can be helpful even for students in higher grades.
Teachers looking to improve their students’ grasp of math, rather than just preparing them for tests, will also find useful insights here.
Why do students start struggling with math in middle and high school?
How does struggling begin?
Many kids do just fine with math in elementary school, so it can be a surprise to parents when things take a turn in middle school. At first, a student might fail one math test. Then another. They might start blaming circumstances—lack of time, noisy classmates, or distractions that made it hard to focus. Next, the blame might shift to the teacher. Eventually, they might say, “I’m just not a numbers person.” In the worst cases, students might even start boasting about being bad at math, convincing themselves and others that math is pointless. So, what went wrong? And where exactly did things start to fall apart?
Why does the struggle start?
Elementary school math feels real and straightforward—counting apples, sheep, and friends. But middle school math dives into the abstract: denominators, equations, and functions. This shift from concrete to abstract math is challenging for many kids, and navigating it successfully requires extra support. Teachers understand this and are equipped to help. But with a packed curriculum, large classes, and a fast pace, they often can’t provide the personalized help every student needs. Now, imagine a student misses a key lesson—maybe they were sick or just had an off day. If those gaps aren’t filled, they’ll try to patch things together themselves. But how do they go about it?
Strategies students use to overcome struggles
Using intuition
In everyday situations, intuition can be helpful. But in math and science, things are often counterintuitive. Take percentages, for example: if the price of an item increases by 50% and then decreases by 50%, many students intuitively think the price returns to its original value. However, this isn’t correct. When intuition fails, students often resort to other strategies like rote memorization.
Rote memorization
Rote memorization is quite a typical approach. For example, when dividing fractions, students often memorize the rule: divide by a fraction by multiplying by its reciprocal. For instance: \[ \frac{1}{3} \div \frac{1}{9} = \frac{1}{3} \times \frac{9}{1} = \frac{9}{3} = 3 \].
It’s much easier to memorize this rule than to understand why it works (explained here ↓). And when memorization seems like the easier path, many students take it without hesitation. However, in the long run, neither intuition nor rote memorization is a sustainable solution. Up next, we’ll explain why.
Why these strategies don’t work
Relying on memorization creates a habit:
“If I don’t understand something, I’ll just memorize it.”
This approach might work through 7th or 8th grade, or even a bit longer, but eventually, it becomes unsustainable:
No one can memorize all of math.
This is also why students often forget what they’ve “learned” so quickly. In reality, they haven’t truly learned it—they’ve only memorized it. Often, the material is forgotten right after the test. And when that happens, here’s what comes next:
What happens next?
When a student forgets everything they just memorized, they have to learn every new math topic as if starting from scratch, without building on previous knowledge.
This forces them to put in enormous effort—yet with very little progress. This creates a vicious cycle. The more they struggle, the more they rely on memorization. With a fast-paced curriculum that moves quickly from one topic to the next, some students soon find themselves unable to follow along at all. So, how can they break out of this cycle?
How to stop struggling and perform better?
Take a step back
As we mentioned earlier, it’s essential to fully understand each topic before moving forward—not just memorize it. But what if gaps in understanding have already formed? The solution is straightforward: take a step (or several) back and figure out where things started to go wrong. That’s exactly why we created this article.
Identify problematic math topics
This article highlights common math mistakes that students often struggle with. When these mistakes aren’t addressed, they can lead to confusion and ineffective strategies, like memorization. Share these topics with your middle or high schooler and ask them to answer related questions. If they answer correctly, they likely understand the material. If not, it may be time to revisit and reinforce the topic.
Address the problems
Once you’ve identified a weak spot, have your child review the correct answers and explore the reasons behind their confusion. We’ve outlined how these mistakes can lead to long-term challenges, impacting future learning, career skills, and even daily life. Most importantly, encourage and motivate your child to tackle these challenges. Next, we’ll share tips on how to keep them motivated.
How to motivate your middle or high schooler to work on it?
As math becomes more abstract, students often ask, “Why do I need to learn this?” The key to keeping them motivated is helping them understand its importance. Math is essential in almost every profession—whether nursing, law, or psychology—and in daily life.
At DARTEF, we show students how math applies to real-world situations with articles and videos that make the connection clear.
Articles are free to access on our blog, and our videos are available for a small fee. Why subscribe?
Common math mistakes that cause struggles
Table of Contents
Introduction
Math topics are organized by grade for easier navigation. However, keep in mind that a topic learned in, for example, grade 6, can often affect the understanding of topics in later grades, such as grades 8 or 9. Therefore, we recommend making sure that foundational topics from earlier grades are also well understood. For instance, if your child is in grade 9, ensure they grasp the key concepts from earlier grades before moving forward. Please note that this is a living article, and we are continually updating it (the latest update was on January 16th, 2025).
Elementary school
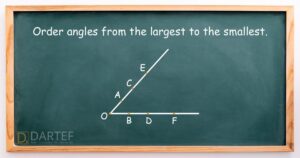
Angles
[Click the picture to enlarge]
Share this quiz with your kid:
All three angles are equal.
Common mistakes:
Some students may believe that angle EOF is the largest because it looks bigger than angles COD and AOB. This happens when they confuse the appearance of an angle with its actual measure, assuming that a visually larger angle is necessarily greater in size. The misunderstanding arises from focusing on the distance between two rays rather than the amount of rotation between them.
Why do these mistakes happen and how to fix them?
One reason for this mistake is that the formal definition of an angle — stating that it is formed by a common vertex and two rays — often doesn’t receive enough attention. As a result, when a student is asked to define an angle, they may use common, everyday language (e.g., “An angle is a corner where two lines meet”), which leads to the loss of the necessary mathematical formalism.
How to fix it: Emphasize that an angle is formed by two rays that share a common endpoint. To describe how an angle is measured, it is helpful to refer to the rotation of the rays around the common point. Use the example of clock hands to illustrate this concept.
Another reason for this mistake is a tendency to rely on the “common representation” of angles typically presented in math classes — one side being horizontal, and the angle opening to the right:
Students become accustomed to this representation, which can create difficulty when encountering other visual representations.
How to fix it: Show various visual representations of angles beyond the “common representation.” For instance, refer to the positions of clock hands at different times. Emphasize that both the 0° (12 o’clock) and 180° (6 o’clock) positions are angles as well. Additionally, highlight that a 0° angle is formed when the two rays overlap without rotation, while a 360° angle is formed after a full rotation.
Why it matters:
In further studies:
A clear understanding of angles is essential for grasping more advanced mathematical concepts. For example, geometry and trigonometry, which students often encounter in middle and high school, rely on the ability to define and measure angles accurately. Misunderstanding basic principles like angle formation can hinder a student’s progress in these subjects, as the concepts build upon each other.
In professional life:
Angles are fundamental in fields such as architecture, engineering, and computer graphics. Professionals in these areas use angles daily, whether in design, structural calculations, or programming.
In daily life:
Understanding angles also plays a role in everyday tasks, such as using tools, reading maps, or even driving. For instance, when navigating with a GPS, recognizing turns as angles helps with directions and navigation. Additionally, some hobbies, like photography or arranging furniture, often involve measuring angles for desired results.
How to motivate a student?
Help your student understand why angles matter by showing how they’re used in real life. Whether it’s in construction, design, or even sports, angles are everywhere! Check out this section on making math relatable and engaging!
Source: [7]
Division
[Click the picture to enlarge]
Share this quiz with your kid:
- Partition (sharing): 8 is divided into two equal parts, each part being 4.
- Measurement (repeated subtraction): 8 ÷ 2 represents how many times 2 can be subtracted from 8 (i.e. 8-2-2-2-2=0, 4 times).
Common mistakes:
Students often only recognize the first way (partitioning) and are surprised to learn about the second way.
Why do these mistakes happen and how to fix them?
This mistake arises because partitioning is intuitive and connects to everyday experiences, such as dividing 8 candies among 4 friends.
Why it matters:
When students rely too heavily on intuition, it can lead to issues in future learning, professional life, and even in daily activities.
In further studies: Understanding repeated subtraction is key to grasping more advanced concepts, such as dividing fractions. For example, 1/3 ÷ 1/9 = 3, because you can subtract 1/9 from 1/3 three times.
In professional life: Repeated subtraction is frequently used in logistics. For example, how many trucks are needed to move 10,000 tons of asphalt, if each truck can carry 25 tons? 10,000 ÷ 25 = 400.
In daily life: Repeated subtraction is helpful in practical tasks. For instance, if you’re building a 120-foot fence and want to space the fence posts 8 feet apart, you’ll find there will be 15 spaces (and 16 posts).
How to motivate a student?
Want to spark your teen’s interest in practical uses of division? Check out this section on making math relatable and engaging!
Geometry
[Click the picture to enlarge]
Share this quiz with your kid:
Square.
Common mistakes:
Sometimes, students may mistakenly call the resulting shape a rhombus or diamond. In reality, when a square is rotated by 45°, it remains a square. Rotation does not change the formal properties of the square.
Why do these mistakes happen and how to fix them?
This mistake arises because students often rely on visual memorization of how shapes appear, while paying less attention to their formal properties.
Why it matters:
Relying too much on visual memorization can lead to challenges in future studies, professional life, and even in daily situations.
In further studies: Students who depend on visual memorization might struggle when they encounter non-standard representations of shapes on exams.
In professional life: In fields like medicine, relying on typical imaging appearances can lead to diagnostic errors. For instance, a radiologist may misdiagnose a disease when its presentation doesn’t “look” like the textbook example, missing subtle but crucial signs.
In daily life: In navigation, someone who memorizes a map’s appearance without understanding cardinal directions or scales might struggle to navigate in unfamiliar areas. Real-world navigation often involves adapting to different perspectives and reorienting oneself based on landmarks—something memorization alone cannot address.
How to motivate a student?
Looking for ways to keep your teen curious about shapes and their properties? Check out this section on fostering curiosity in math. ↑
Source: [1]
Grade 6
Divide fractions
[Click the picture to enlarge]
Share this quiz with your kid:
Because you can multiply by any non-zero number (not just a reciprocal), the resulting answer will always be the same.
Common mistakes:
Some students (and even some adults) simply say, “It’s a rule we were taught in school,” without understanding the reasoning behind it.
Why do these mistakes happen and how to fix them?
As in similar cases, memorizing this rule often seems like the easiest way to get through the problem. However, in the long run, it creates a habit of memorizing the rule without truly understanding it.
The logic behind division by a fraction is quite straightforward and can be explained using an algebraic approach. The key idea is that you don’t have to multiply by the reciprocal—you can multiply by any non-zero number. Here’s how it works:
Suppose we need to solve the following:
\[
\frac{1}{3} \div \frac{1}{9}.
\]
We know we can multiply both the numerator and denominator of a fraction by the same non-zero number without changing its value. Let’s choose to multiply by 18:
\[\left(\frac{1}{3} \cdot 18\right) : \left(\frac{1}{9} \cdot 18\right)\]
Simplifying this:
\[\frac{18}{3} \div \frac{18}{9} = 6 \div 2 = 3.\]
The answer is 3.
Now, let’s try multiplying by another number, say 90:
\[\left(\frac{1}{3} \cdot 90\right) : \left(\frac{1}{9} \cdot 90\right)\]
Simplifying:
\[
\frac{90}{30} \div \frac{90}{9} = 30 \div 10 = 3.
\]
The answer is still 3.
Finally, let’s apply the rule taught in school, multiplying by the reciprocal of the second fraction:
\[
\frac{1}{3} \div \frac{1}{9} = \left(\frac{1}{3} \cdot 9\right) : \left(\frac{1}{9} \cdot 9\right) = \frac{9}{3} \div 1 = 3.
\]
The reciprocal simplifies the second fraction to 1 (i.e., \( \frac{1}{9} \times 9 = 1 \)). Once this simplification happens, it no longer affects the result, because dividing by 1 doesn’t change the value. What remains is simply the dividend, which gets multiplied by the reciprocal of the second fraction. This is how the rule of multiplying by the reciprocal works, turning the division into a straightforward multiplication.
Key takeaway:
When dividing by a fraction, you can multiply both the dividend and divisor by any non-zero number, then simplify the resulting fraction. Multiplying by the reciprocal is just a convenient way to reduce the divisor to 1.
Why it matters:
- In further studies:
Understanding how to correctly divide by fractions is fundamental for progressing in math, especially in algebra, calculus, and higher-level subjects. A strong grasp of this concept is essential for students when they encounter more advanced topics, such as rational expressions and equations. - In professional life:
In various professions, especially in fields like engineering, finance, and computer science, working with fractions is common. For example, when calculating material quantities, converting units, or analyzing data. - In daily life:
While the need to divide by fractions in daily life may not seem obvious at first glance, understanding the concept can significantly simplify various DIY tasks, such as carpentry or construction projects—whether measuring spaces or cutting materials.
How to motivate a student?
Looking for ways to keep your teen curious about learning math? Check out this section on fostering curiosity in math. ↑
Equalities
![On the green chalkboard, it is written: 'Fill in the missing number: 8 + 4 equals [blank] plus 5.'](https://dartef.com/wp-content/uploads/2024/11/equality1.jpg)
[Click the picture to enlarge]
Share this quiz with your kid:
7
(because the left side of the equation must always equal the right side.)
Common mistakes:
Sixth graders sometimes misunderstand the equality sign (=) and see it as “and the answer is.” This confusion can lead them to give answers like 12 (thinking 8 + 4 = 12) or 17 (thinking 8 + 4 + 5 = 17).
Why do these mistakes happen and how to fix them?
In elementary school, students often memorize the visual pattern of “digit + digit = answer.” When they encounter equations in higher grades, this visual memory can conflict with their understanding of equality and algebraic equations, where both sides must balance, not just the addition of the numbers.
Why it matters:
- In further studies:
Understanding equalities is crucial for grasping concepts like systems of linear equations. When substituting expressions, it’s essential that equality is maintained to ensure the solution is accurate. - In professional life:
A key example of equalities in the financial sector is the basic accounting equation: Assets = Liabilities + Equity. This equation helps companies ensure their financial records are balanced and accurate, forming the foundation of financial reporting and analysis. - In daily life:
In health and nutrition, understanding equalities can help in planning a balanced diet. For instance, it allows for precise calculations of calories and helps adjust meal portions according to individual nutritional needs, contributing to healthier living.
How to motivate a student?
Looking for ways to keep your teen curious about the equality sign and balancing equations? Check out this section on fostering curiosity in math. ↑
Source: [3]
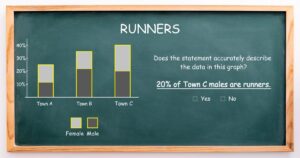
Percentages
[Click the picture to enlarge]
Share this quiz with your kid:
No. The correct interpretation is: “20% of ALL RUNNERS are males from Town C.”
Common mistakes:
Students often mistakenly agree with the incorrect statement “20% of Town C males are runners.”
Why do these mistakes happen and how to fix them?
This mistake is common among students learning about percentages. The issue often stems from misinterpreting the graph. The incorrect statement “fits” with the visual cue of 20% on the graph, leading students to choose it without fully analyzing the data.
- Start by saying: “Don’t rush to choose the answer that seems to fit well.”
- Ask: “What does the graph actually show?”
The correct answer here is: “The distribution of runners from towns A, B, and C.” - Clarify the “whole” being represented.
Stress that percentages depend on what constitutes the “whole.” In this case, the whole is “all runners”, not “Town C males”.
Why it matters:
- In Further Studies:
Percentages and ratios are essential in many subjects, including physics (e.g., efficiency calculations), chemistry (e.g., concentration percentages), and biology (e.g., population studies). - In Professional Life:
Accurate data interpretation is vital in almost every job. For example, in marketing, avoiding errors like the Simpson’s Paradox is important when analyzing customer behavior trends. - In Daily Life:
Understanding percentages and graphs is essential for daily tasks like voting on policies, where graphs might show the distribution of budget allocations or public opinion percentages.
How to motivate a student?
Looking for ways to keep your teen curious about percentages and graphs? Check out this section on fostering curiosity in math. ↑
Sources: [4] and [5].
Subtracting negatives
[Click the picture to enlarge]
Share this quiz with your kid:
When you subtract −1, it’s like removing a negative value. Taking away −1 is the same as adding 1, because you’ve removed the “negative” part.
Common mistakes:
It’s just a rule!
Some students, unsure of why this happens, simply say, “It’s just a rule,” without understanding the logic behind it.
Why do these mistakes happen and how to fix them?
While subtracting a negative makes logical sense, many students opt to memorize the rule “minus and minus gives a plus” because it’s easier to remember than to truly understand the concept. To help students grasp the underlying idea, practical examples can be very effective. For instance, using scenarios like “removing a debt” or a “temperature rebound” illustrates the core principle of subtracting negatives. Another helpful visualization is using “positive” and “negative” weights with props, such as a weight and a balloon, to show how negative numbers behave in real life.
To explain this concept further, we have created the following video:
Why it matters:
- In Further Studies:
When students later learn about multiplying or dividing negatives, they might continue to rely on memorization. This habit can make it harder for them to grasp why “Minus times minus gives a plus” actually works. - In Professional Life:
Working with negative numbers is essential in many professions. They appear in accounting (balancing budgets), construction engineering (calculating loads), telecommunications (managing signal strength), and countless other fields. Understanding how to operate with negatives accurately ensures reliable results and prevents costly mistakes. - In Daily Life:
Grasping how negative numbers work is key for everyday tasks, from managing finances to interpreting weather forecasts. For instance, if the forecast mentions that a “drop of -5°F will rebound,” it means the temperature will rise by 5°F. Without a solid understanding of negatives, simple calculations and interpretations can become unnecessarily confusing.
How to motivate a student?
Looking for ways to keep your teen curious about subtracting negatives? Check out this section on fostering curiosity in math. ↑
Zero
[Click the picture to enlarge]
Share this quiz with your kid:
8, 110, and 0.
Common mistakes:
Students often identify only 8 and 110 as even numbers, excluding 0. In reality, 0 is even because it is divisible by 2 (0 ÷ 2 = 0).
Why do these mistakes happen and how to fix them?
This widespread misunderstanding stems from how zero is introduced in elementary school, often described as “nothing.” This leads to the false belief that “nothing” cannot be divisible, and thus, 0 is neither even nor odd.
Why it matters:
Understanding zero as a number, not as “nothing,” is crucial for further studies, technology, professional applications, and daily life.
- In further studies: In trigonometry, recognizing that a triangle’s leg can have a zero length is important, e.g., cos 90°=0.
- In professional life: In fields like information technology, zero often represents “FALSE” in programming (opposite to “TRUE”), while in accounting, zero indicates a balanced budget, not an absence of value.
- In daily life: Zero degrees on a temperature scale (e.g., 0°F or 0°C ) represents a specific point, not “nothing”.
How to motivate a student?
Looking for ways to keep your teen curious about zero and its properties? Check out this section on fostering curiosity in math. ↑
Source: [2]
Grade 7
Probability
[Click the picture to enlarge]
Share this quiz with your kid:
Getting the pair 5-6.
The probability of rolling a specific pair with two dice depends on the number of possible outcomes:
- Pair 5-6: There are two favorable outcomes—rolling a 5 on the first die and a 6 on the second, or vice versa. The probability is calculated as:
\( 2 \times \frac{1}{6} \times \frac{1}{6} = \frac{2}{36} = \frac{1}{18} \).
- Pair 6-6: There is only one favorable outcome—rolling a 6 on both dice. The probability is:
\( \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} \).
Therefore, the pair 5-6 is twice as likely to occur as the pair 6-6.
Common mistakes:
Many students mistakenly believe that both pairs, 5-6 and 6-6, have the same chance of occurring.
Why do these mistakes happen and how to fix them?
This mistake arises from relying on intuitive thinking and interpreting the problem using everyday language. For example, when students read “Getting the pair 5-6,” their intuition may assume that the first die must show 5 and the second must show 6. However, in mathematical terms, “the pair 5-6” means that either die could show 5 while the other shows 6.
To correct this misunderstanding, emphasize the distinction between intuitive and mathematical thinking. Encourage students to explicitly analyze the problem in writing, which forces them to use mathematical reasoning rather than intuition. By solving problems systematically on paper, students can better grasp concepts like order and combinations, reducing reliance on incorrect assumptions.
This approach not only clarifies specific probability concepts but also helps build habits that prevent similar mistakes in other areas of math.
Why it matters:
- In further studies: A solid understanding of probability concepts is crucial for further studies. In fields such as statistics (taught in high school) or computer science (studied in college), understanding probability builds a foundation for more complex topics like statistical inference or machine learning. Misunderstanding simple probabilities, like the example with dice, can lead to misconceptions that affect a student’s ability to grasp more advanced concepts later on.
- In professional life:
Probability is used extensively in a variety of fields, and with the growing development of artificial intelligence, the importance of properly understanding probability is increasing. For example, specialists developing various digital services rely on probability analysis to optimize user experiences and ensure product success. - In daily life: Understanding probability also helps in making informed decisions in everyday life. Whether determining the chances of weather conditions, understanding odds in games, or evaluating risks (e.g., buying insurance or planning for future events), probability plays a significant role in helping us make more informed choices
How to motivate a student?
Want to help your teen grasp the importance of probability and develop a deeper interest in math? Relate it to real-life scenarios! Explore this section for tips to keep math engaging and relevant. ↑
Source: [6]
Grade 8
Linear equations
[Click the picture to enlarge]
Share this quiz with your kid:
This equation can be rewritten by combining like terms into the form 2x−5=0
- The variable is x.
- The coefficient of x is 2.
- The constant is −5
Common mistakes:
Some students might correctly identify “x” as the variable and “2” as the coefficient but incorrectly state that the constant is “3”, ignoring the “8” in the equation. Additionally, some may claim the constant is “5” but forget to include the negative sign.
Why do these mistakes happen and how to fix them?
These errors often stem from a partial understanding of the topic. Students might visually memorize the general form of a linear equation, mx+b (e.g., 2x+3), and focus only on the terms before the equals sign, neglecting the term on the other side.
How to fix it:
Present linear equations in various non-standard forms, such as:
- x+x+1+1+1=8
- x+x−x+x+5−2-8=0
- 4x+2=2x−1+8
Ask students to transform these equations into their standard form to demonstrate that they represent the same equation. This practice helps reinforce the importance of considering all terms, including those after the equals sign.
Why it matters:
In further studies: A strong understanding of the components of linear equations—variables, coefficients, and constants—is critical as students progress to more complex algebra topics, such as solving systems of equations, inequalities, and quadratic equations. These concepts build on each other, and mastering the basics ensures students don’t struggle with more advanced material.
In professional life:
Linear equations are used in a variety of fields such as economics, engineering, and computer science. Professionals rely on solving these equations for tasks like financial modeling or lighting design. A solid understanding helps professionals make accurate predictions and decisions based on mathematical models, avoiding costly mistakes.In daily life:
Recognizing the components of linear equations can help in everyday situations, such as budgeting, planning, or interpreting data. For example, understanding how costs grow linearly over time can help individuals make better financial decisions, like planning for savings or estimating expenses. Linear thinking also helps in making logical connections and organizing tasks more efficiently.
How to motivate a student?
Want to help your teen grasp the importance of linear equations? Show them how these concepts are used in real-life problem solving! Explore this section for tips on making math more engaging and relevant, helping your student see the practical value of mastering the basics. ↑
Source: [8]
Grade 9
Trigonometry
[Click the picture to enlarge]
Share this quiz with your kid:
In a right-angled triangle, sine is defined as the ratio of the length of the opposite side to the hypotenuse:
\[
\sin(X) = \frac{\text{opposite}}{\text{hypotenuse}}
\]
Since the hypotenuse is always the longest side of a triangle, the opposite side cannot exceed its length. Therefore, \( \sin(X) \) cannot be greater than 1.
Common mistakes:
“Because the teacher said so!”
Some students simply accept the rule “Sine cannot be greater than 1” without questioning or understanding the reasoning behind it.
Why do these mistakes happen and how to fix them?
Although the correct explanation is often shared with students, many prefer to memorize the rule “Sine cannot be greater than 1” because it seems simpler. Visual aids like:
\( 0 \leq \sin(X) \leq 1 \)
or the generalized form:
\( \sin(X) \in [-1, 1] \)
can also stick in students’ visual memory. While helpful initially, this reliance on memorization can hinder a deeper understanding of trigonometric functions like sine and cosine, making it harder to grasp their broader applications in mathematics and beyond.
Why it matters:
- In further studies: A solid understanding of trigonometry fundamentals is critical for exploring more advanced topics in math and science. For instance, in mathematics, the range of sine values is a cornerstone concept for mastering the unit circle. In physics, trigonometry underpins topics like motion, forces in mechanics, and wave behavior.
- In professional life: Trigonometry plays a key role in real-world problem-solving within fields like engineering and architecture. For example, understanding sine and cosine limits ensures the accurate design of roof overhangs.
- In daily life: Though trigonometry’s use outside professional fields is limited, it can greatly simplify hobby and DIY activities, such as building a perfect foundation for a house or creating perfectly squared vegetable patches.
How to motivate a student?
Want to help your teen grasp the essence of trigonometry? Show how it connects to real-world problems! Explore this section for tips to keep math engaging and relevant. ↑
References
- Rafiah, H., & Ekawati, A. (2017, May). Misconceptions of the students with high mathematical creative thinking level in solving the geometric shapes problems. In 5th SEA-DR (South East Asia Development Research) International Conference 2017 (SEADRIC 2017) (pp. 155-158). Atlantis Press.
- Arai, N. H., Sugawara, S., & Matsuzaki, T. Misconception about Zero: How Difficult it is to Overcome. The 15th International Congress on Mathematical Education Sydney, 7-14 July, 2024
- Falkner, K., Levi, L., & Carpenter, T. (1999). Early childhood corner: children’s understanding of equality: A foundation for algebra. Teaching children mathematics, 6(4), 232-236.
- Schield, M. (2006). Statistical literacy survey analysis: Reading graphs and tables of rates and percentages. In Proceedings of the Sixth International Conference on Teaching Statistics.
- Rakes, C. R. (2010). Misconceptions in rational numbers, probability, algebra, and geometry. University of Louisville.
- Fischbein, E., & Schnarch, D. (1997). Brief report: The evolution with age of probabilistic, intuitively based misconceptions. Journal for research in mathematics education, 28(1), 96-105.
- Ünal, D. Ö., & Ürün, Ö. (2021). Sixth grade students’ some difficulties and misconceptions on angle concept. Eğitimde Nitel Araştırmalar Dergisi, (27), 125-154.
- Yansa, H., Retnawati, H., & Janna, M. (2021, May). Misconceptions of basic algebra on linear equation in one variable material. In Journal of Physics: Conference Series (Vol. 1882, No. 1, p. 012091). IOP Publishing.