Table of Contents
Quick reminder of what algebraic and rational expressions are
Algebraic expressions are mathematical phrases that can include numbers, variables, and operation symbols. For instance:
\(3x + 5\),
\(2x^2 – 4xy + y^2\),
\(7a + b – c\)
are all algebraic expressions. These expressions can be simplified or evaluated by substituting values for the variables.
Rational expressions, on the other hand, are a specific type of algebraic expression that represent the ratio of two polynomials. For example:
\(\frac{3x}{x+2}\)
\(\frac{2x^2 – 4x + 6}{x^2 – 1}\)
are rational expressions. Simplifying rational expressions often involves factoring polynomials and reducing them to their simplest form. Both algebraic and rational expressions are fundamental in algebra, providing the tools for solving equations, modeling real-world scenarios, and analyzing relationships between variables.
Algebraic and rational expressions in real life
There is a real-life need to find the values of algebraic and rational expressions and simplify them. Understanding the connection between this mathematical topic and its real-world applications will help you grasp the subject better and show how it relates to various jobs.
Examples of Real-Life Use of Algebraic and Rational Expressions
Historically, algebraic and rational expressions were used for various calculations. As technology developed, many of these calculations, once done manually by people, are now performed by computers. Today, computers are used in almost every aspect of our lives, including agriculture, transportation, construction, and managing important infrastructure like water and electricity supply. Computers run special programs to control these systems, and these programs often contain algorithms with algebraic and rational expressions. Below are some examples:
Algebraic and Rational Expressions in Car Safety Systems
In car safety systems, such as when a car needs to perform emergency braking, the car computer must make decisions very fast, in microseconds. Various formulas and expressions are used to calculate movement paths and predict collisions. Simplifying these expressions makes the calculations faster and more efficient.
Algebraic and Rational Expressions for Air Traffic Control
In the control systems of aircraft and air traffic control, special computers constantly monitor various parameters that affect the safety of aircraft. Calculating the values of algebraic and rational expressions helps determine flight times and avoid collisions. Simplifying these expressions speeds up these crucial calculations.
Algebraic and Rational Expressions for Critical Infrastructure
In critical infrastructure systems, such as nuclear power plants, safety systems like reactor protection or cooling systems rely heavily on sensors and computer algorithms. These algorithms involve algebraic and rational expressions to calculate critical parameters. Simplifying these expressions ensures that necessary calculations are done quickly, ensuring stable operation.
Algebraic and Rational Expressions for Battery-Powered Systems
In various battery-powered mini computers, like sensors or drones, navigation algorithms involve recognizing obstacles and calculating distances. These algorithms use algebraic and rational expressions. Simplifying these expressions reduces the energy needed for calculations, extending battery life.
To better understand how algebraic and rational expressions help perform these controls, let’s look at a case study.
Case Study: "Speeding up computer work via simplification of rational expressions"
Introduction
To see a real-life case of how simplifying expressions helps speed up computer work, let’s take a brief look at the early days of computers. The first electronic computers, which emerged in the mid-20th century, were extremely large, often filling entire rooms in buildings. Initially, these computers were primarily used for military applications, such as calculating missile trajectories based on specific expressions and formulas. One such example is the ENIAC computer, considered the world’s first electronic computer, constructed in 1945:

Time Needed for Calculation of Expression Value
Aside from their size, these computers were also remarkably slow, often requiring significant time to calculate values of expressions. Below, you can observe an actual expression used for calculating missile aerodynamics on the ENIAC computer:

In the 1940s, it took approximately 5 minutes to compute the value of this formula. Why so long? Because every mathematical operation performed on a computer requires a certain amount of time for its execution. For example, a single multiplication took several seconds of computer time. While this might not seem like much, calculating just one missile trajectory required nearly 1000 multiplications. If each multiplication took several seconds, then 1000 of them could take several minutes. But since the military usually needed to calculate thousands of different trajectories, without simplifying the formulas, this process would have taken months or even years. And this is where simplification of expressions comes to the rescue. Let’s take a more detailed look.
Calculating Non-Simplified and Simplified Expressions
How to Measure Time for Calculation of Expression Value?
In this example, we will use a special simulation program to measure how much time computers from different eras needed for calculating the values of algebraic and rational expressions. Below is a screenshot of this simulation program:
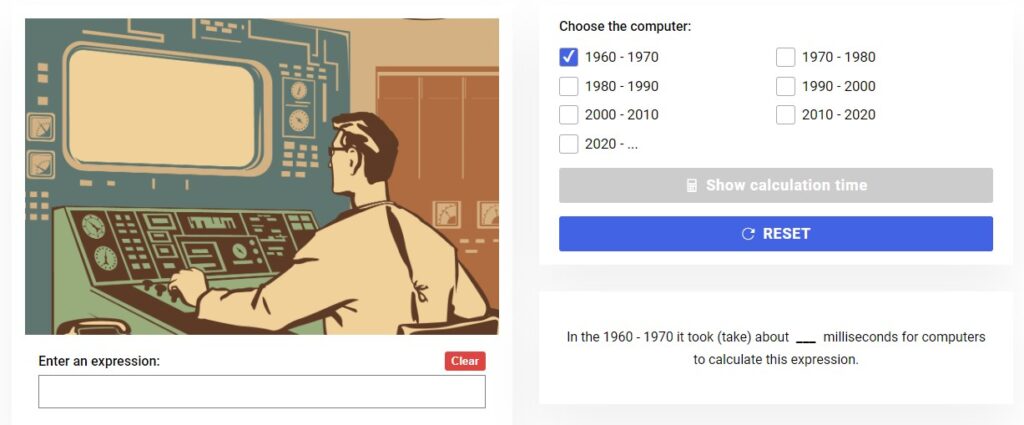
Next, let’s calculate the value of the non-simplified rational expression.
Calculating the Value of Non-Simplified Rational Expression
Let’s ask the computer from the 1960s to calculate the value of the following rational expression when a=500 and b=800. :
\(\frac{{a^2}}{{a+b}} – \frac{{a^3}}{{a^2 + 2ab + b^2}}\)
Next, let’s simulate the calculation in the simulation program, with a=500 and b=800. The value of the expression is approximately 118.34, and the calculation time is 2880 milliseconds (approximately 2.9 seconds).
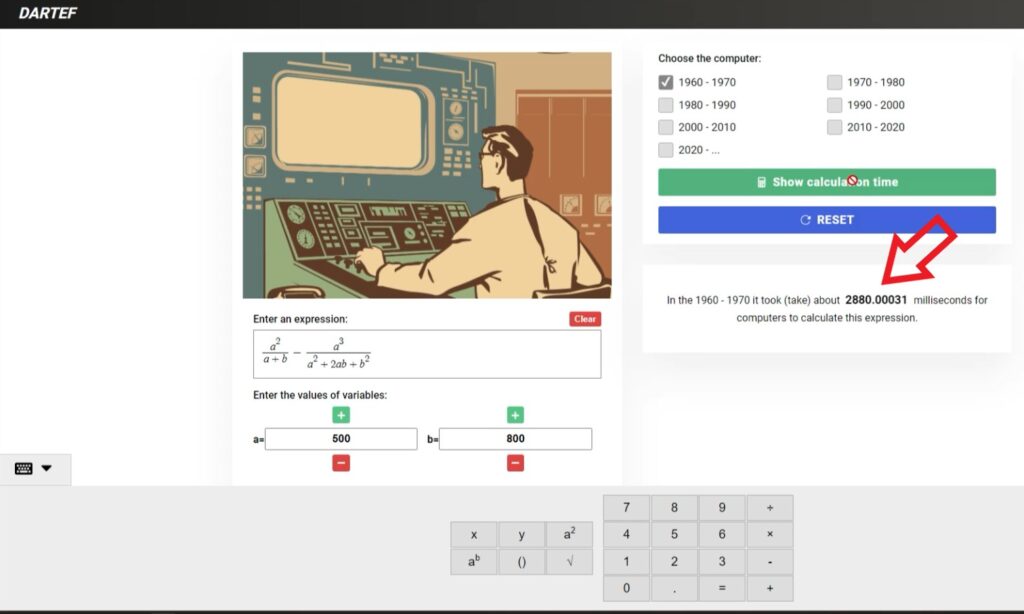
Next, let’s simplify this expression and then calculate its value again.
Calculating the Value of Simplified Rational Expression
Let’s simplify this rational expression as follows:
\(\frac{{a^2}}{{a+b}} – \frac{{a^3}}{{a^2 + 2ab + b^2}} = \frac{{a^2}}{{a+b}} – \frac{{a^3}}{{(a+b)^2}} = \frac{{a^2(a+b)}}{{(a+b)^2}} – \frac{{a^3}}{{(a+b)^2}} = \frac{{a^2(a+b) – a^3}}{{(a+b)^2}} = \frac{{a^3 + a^2b – a^3}}{{(a+b)^2}} = \frac{{a^2b}}{{(a+b)^2}}\)
In simplified form, the value of the expression remains the same (approximately 118.34), but the calculation time has decreased from 2.9 seconds to 1 second, which is almost 3 times faster for computers from the 1960s!
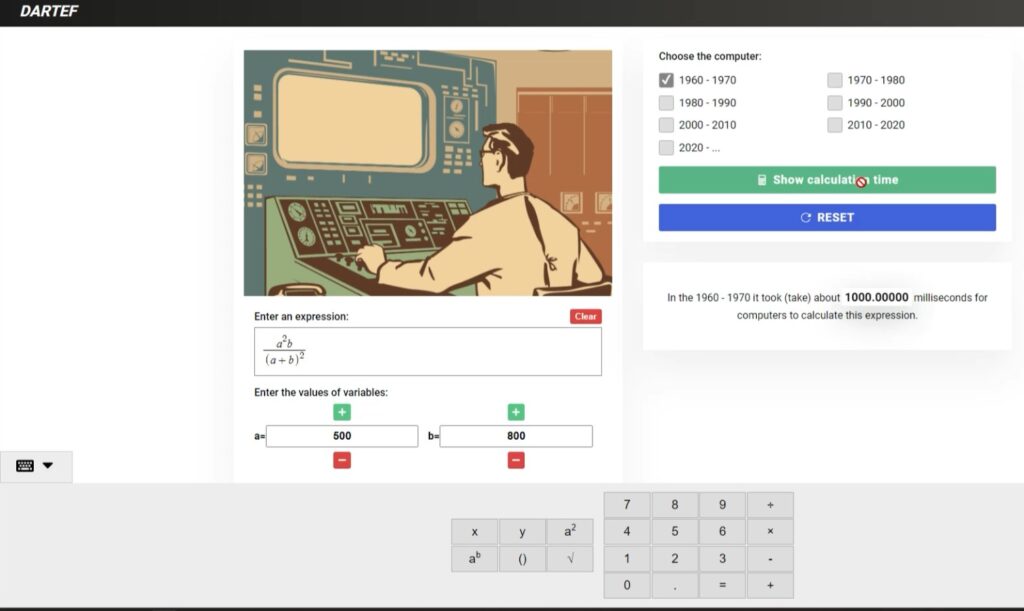
If one had to perform thousands of these calculations, simplifying expressions could save hours, days, or even months of calculation time. Therefore, simplifying expressions in the early days of computers was necessary to make various calculations faster and save time.
However, you may ask, with today’s powerful computers capable of performing several million calculation operations per second, is simplification of expressions still important?
Simplification of Expressions Nowadays
It’s true that computers today are very fast. However, as we explained earlier, in modern technology, we have many time-critical applications where calculation time must be as swift as possible. Car safety systems, aircraft safety and control systems, critical infrastructure control, and battery-powered systems are just a few examples where simplification of algebraic and rational expressions and calculating their values are crucial.
People who work with such critical systems are often referred to as mission-critical engineers or reliability engineers. Many of these specialists studied computer science because today’s mission-critical systems heavily rely on computers. Therefore, if you’re considering a career in computer science and want to work with mission-critical systems, then studying rational expressions is crucial for you.
Classroom version: Engage your students with real-world examples
If you want to share these examples with your students in math class, we have a full version of the video available. This video explains the examples in just a few minutes and helps students connect what they learn in school with real-world applications. It also shows them how math is used in various jobs.
Video preview:
References
For preparing this article, we used genuine documentation of the ENIAC computer:
Additionally, the following two scientific publications were used:
Further reading
Algebraic and rational expressions, polynomials, and formulas are widely used in a variety of domains. Below are some other articles from DARTEF that explain their usage in real life:
- The article “Polynomials: A Real-Life Example (from Marketing)” explains how finding the value of polynomials helps to make informed business decisions for marketers.
- The article “Dependent and Independent Variables: A Real-Life Example (from Fire Protection)” explains how algebraic expressions and formulas with multiple independent variables are used to predict the spread of wildfire.
