Subtracting negative numbers: video version
Would you like to explore this example through a short video? The video explains the rule behind subtracting a negative using an animated example of a scale.
Prefer text? Just keep reading!
Subtracting negative numbers: text version
Rethinking the concept of zero
To understand why subtracting a negative number results in adding a positive, we first need to rethink the idea of zero. Many people think of zero as simply “nothing” or “emptiness.” That’s partly true—but not the full picture. Zero can also mean something is “balanced” or “cancelled out.” Let’s look at a few examples.
+1 and -1 dollars
Imagine you have 1 dollar in your pocket, but you owe a friend 1 dollar. In total, you have zero dollars. But that doesn’t mean you have “nothing.” You actually have +1 dollar (in your pocket) and -1 dollar (as debt). These are balanced: +1 and -1 cancel each other out, so:
\[
\underbrace{+1}_{\text{in your pocket}} + \underbrace{(-1)}_{\text{your debt}} = \underbrace{0}_{\text{total amount you have}}
\]
Now imagine your friend says, “You helped me yesterday, so I’m canceling your debt—keep the dollar.” That means you can subtract the -1 dollar (your debt):
\[
\underbrace{+1}_{\text{in your pocket}} + \underbrace{(-1)}_{\text{your debt}} – \underbrace{(-1)}_{\text{debt removed (subtracting a negative!)}} = \underbrace{+1}_{\text{in your pocket}}
\]
So subtracting a negative dollar canceled your debt and let you keep the dollar in your pocket.
See how thinking of zero as “balance” helps explain why subtracting a negative equals adding a positive?
Scale example 1
Another way to think about balance and zero is using a scale. In the picture below, you see two scales—one with no weights on it, and one with equal weights on both sides.


In both cases, the scale shows zero. This is a good way to understand that zero doesn’t always mean “nothing.” It can also mean that both sides are in balance.
Now let’s take this idea further and modify the scale a little.
Adding and subtracting negative numbers
Scale example 2
This modified scale doesn’t have two plates. Instead, it has two hooks—one pulling downward and the other upward. As we’ll see in a moment, these will represent positive and negative weights.

Adding a positive number
Right now, the scale shows zero because there’s nothing on it—this is the case where zero means “nothing.” Now, let’s add a 1-ounce weight:
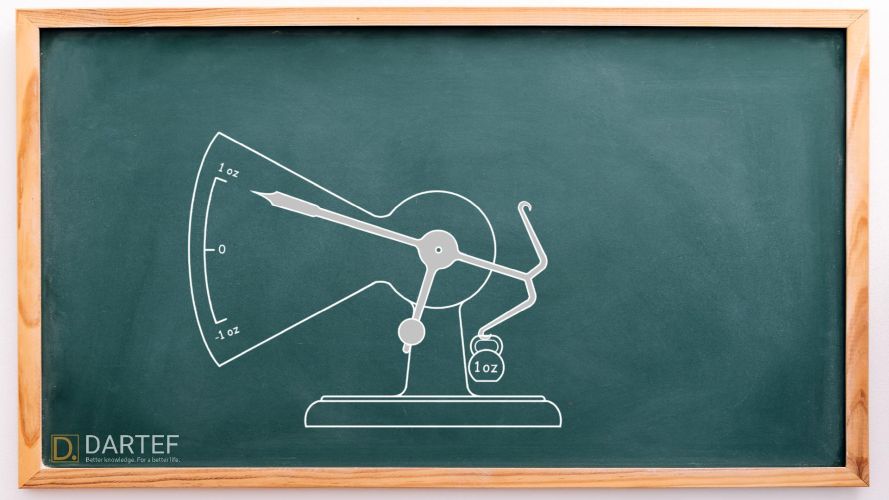
The scale moves down and shows +1 ounce. In math terms, we just did this:
\[
0 + \underbrace{1}_{\text{adding weight}} = \underbrace{+1}_{\text{total}}
\]
Adding a negative number
Now let’s balance it out. We attach a balloon that can lift 1 ounce.

Since the balloon pulls upward, it acts like it has a “negative weight” of -1 ounce. When we add it, the scale moves back to zero:
\[
\underbrace{+1}_{\text{added weight}} + \underbrace{(-1)}_{\text{adding a balloon}} = \underbrace{0}_{\text{total}}
\]
Just like with the earlier scale, we don’t have “nothing”—we have +1 ounce (weight) and –1 ounce (counterweight), and they cancel each other out.
Subtracting a negative number
We’ve finally reached the core of the rule. Let’s remove the balloon to “subtract” a negative weight:
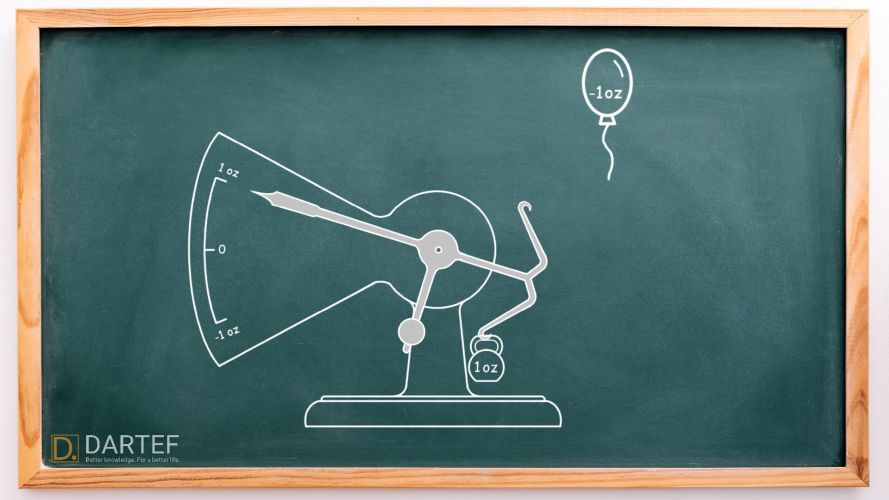
The scale shows +1 ounce again. In math terms, we’ve just done this:
\[
\underbrace{+1}_{\text{added weight}} + \underbrace{-1}_{\text{added balloon}} – \underbrace{(-1)}_{\text{removing balloon (subtracting a negative!)}} = \underbrace{+1}_{\text{positive weight remains}}
\]
Key takeaway:
So why does subtracting a negative number end up adding a positive? Because when you subtract a negative, you’re removing a negative value—which means you’re “releasing” the positive value that was being held back by it. So the result is adding that positive value.
Real-life examples of subtracting negatives
Understanding this rule isn’t just useful in math class—it’s also something professionals use in their jobs. Here are a few examples:
Accounting
In accounting, zero can mean “nothing,” like no money or no debt. But more often, zero means “balanced”—for example, when a company’s assets (positive values) equal its liabilities (negative values). This is called a Balance Sheet. Subtracting a negative here means the company’s debt goes down.
Meteorology
In weather forecasting, the chance of thunderstorms often depends on the temperature difference between air masses. These temperatures can be negative, especially at high altitudes. Meteorologists subtract negative numbers to understand how stable or unstable the atmosphere is.
We’ve written a detailed article on this too: “Subtracting Negative Numbers: A Real-Life Example (from Weather Forecast)”.
Subtracting negatives in further school studies
First of all—understanding why subtracting a negative gives a positive deepens your understanding of zero. As we explained earlier, zero isn’t just “nothing,” it can mean “balance.” This idea comes up in other subjects too:
- In physics, when an object isn’t moving, it usually means all the forces acting on it cancel out to zero. It’s not that there are no forces—just that they balance each other.
- In chemistry, you’ll learn how to balance chemical equations. This means making sure the number of atoms on the left and right sides of the equation are equal—so they “cancel out” just like numbers do.
Conclusion
It’s great that you want to understand what’s behind the rule “subtracting a negative means adding a positive.” Knowing the reason behind the rule is important. Memorizing the rule might help on homework, but real-world problems require real understanding. We hope this article helped explain it clearly!
Is there another math rule you’d like to understand better—like “Why can’t you divide by zero?” Send us a message, and we’ll try to write an article about it!
